입실론-그리디 정책은 탐색과 활용을 적절히 활용하기 위한 기법이다.
하지만 그 결과는 '완벽한 최적 정책'이 아니다.
왜냐하면 '탐색'의 과정을 거쳐야 하고, 그 과정이 비효율이 되기 때문이다.
여기서 '활용'만 하고 싶다는 욕심이 생길 수 있다.
몬테 카를로 법을 이용해, 완벽한 최적 정책을 학습하는 방법을 알아보자.
On-Policy
- 스스로 쌓은 경험을 토대로 자신의 정책을 개선하는 방식이다.
- 밴디트 문제에서 구현한 입실론 그리디 정책에선 '탐색' 과정이 필수로 들어가왔다.
Off-Policy
- 자신과 다른 환경에서 얻은 경험을 토대로 자신의 정책을 개선하는 방식이다.
- 만약, 평가와 개선의 대상인 정책과, 실제 행동을 선택하는 행동 정책을 구분하면 어떻게 될까?
- 이렇게 하면, 실제 행동을 선택하는 'Target policy'에서는 탐색 과정을 제외시킬 수 있을 것 같다!
역할 측면에서 보면 에이전트의 정책은 두가지다.
Target Policy(대상 정책): 평가와 개선의 대상으로서의 정책 (딥러닝에서의 테스트 데이터 역할)
Behavior Policy(행동 정책): 에이전트가 실제로 행동을 취할 때 활용하는 정책 (딥러닝에서의 트레이닝 데이터 역할)
정책과 데이터를 일대일 매칭시키는 것은 엄연히 말하자면 맞지 않지만, 대강 느낌만 잡아가길 바란다.
그래서 오프 정책에서는 Behavior Policy 에서는 '탐색'을, Target Policy에서는 '활용'을 목표로 개선할 수 있다.
다만, Behavior Policy 에서 얻은 샘플 데이터로부터 Target Policy와 관련된 기댓값을 계산하는 방법은 고민을 좀 해봐야 할 것이다.
그래서 등장하는 것이 '중요도 샘플링'기법이다.
중요도 샘플링(Importance Sampling)
중요도 샘플링은 어떤 확률 분포의 기댓값을 다른 확률 분포에서 샘플링한 데이터를 사용하여 계산하는 기법이다.
예를 들어, x라는 확률 변수와 실제 x의 확률은 pi(x)로 표현한 확률 분포의 기댓값 E를 계산해보자.
아마 식을 아래와 같이 세울 것이다.

이 기댓값을 몬테카를로법으로 근사하려면 x를 확률 분포 pi에서 샘플링하여 평균을 내면 될 것이다.
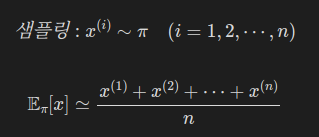
우리는 x가 다른 확률 분포에서 샘플링된 경우의 문제를 풀고자 한다.
예를 들어 x가 (pi가 아닌) b라는 확률 분포에서 샘플링되었다고 가정해보자.
이 경우에 기댓값 E는 어떻게 근사할 수 있을까?
해결의 열쇠는 다음과 같은 식 변형에 있다.

다음과 같이 b(x)의 형태로 바꾸면, 확률 분포 b(x)에서의 기댓값으로 간주할 수 있다.
즉, 아래와 같이 식 변형이 되는 것이다.

이 수식을 통해, 확률분포 pi에 대한 기댓값을 확률분포 b에 대한 기댓값으로 표현했다.
여기서, 위에 있는 분수를 다음과 같이 치환해두자.

이렇게 해두면, 각각의 x에는 가중치로서 함수 rho가 곱해진다고 볼 수 있다.
위 식에 근거하여 몬테카를로법을 수식으로 표현해보자.

이제 다른 확률 분포 b에서 샘플링한 데이터를 이용하여 pi의 기댓값 E를 구할 수 있다.
실전: 중요도 샘플링 코드로 해보기
우리는 다음과 같은 확률 분포를 대상으로 중요도 샘플링을 수행해보자.
pi
| 1 | 2 | 3 |
|---|---|---|
| 0.1 | 0.1 | 0.8 |
b
| 1 | 2 | 3 |
|---|---|---|
| 1/3 | 1/3 | 1/3 |
먼저 확률분포 pi의 기댓값을 일반적인 몬테카를로법(중요도 샘플링 X)으로 구해보자.


참값과 어느정도 유사하게 나온것을 알 수 있었다.
이제 중요도 샘플링을 이용하여 기댓값을 구해보자.


얼추 참값과 유사한 값이 나오긴 했다.
근데 분산이 9.55로, 몬테 카를로 때보다 분산이 훨씬 큰 것을 확인할 수 있었다.
이건 이따가 개선해보자.
이 원리는 다음과 같다.
예시로 3이 샘플링된 경우를 생각해보자.

- 확률 분포 pi를 기준으로 했을 때 3은 대표적인 값이기 때문에, (원래는) 3이 많이 샘플링되어야 한다.
- 하지만 확률 분포 b에서는 3이 특별히 많이 선택되지 않는다.
- 이 간극을 메우기 위해 3이 샘플링된 경우, 그 값이 커지도록 '가중치' rho(2.4)를 곱하여 조정한다.
그런데 샘플링된 값은 3인데, 가중치를 곱해 7.2로 취급한다면, 그리고 만약 지금이 첫 번째 샘플 데이터라면, 현 시점의 추정값은 7.2가 된다는 문제가 생긴다.
이처럼 실제 얻은 값에 부여하는 가중치 rho의 보정 효과가 클수록 분산이 커진다.
그렇다면 어떻게 해야 분산을 줄일 수 있을까?
방법은 b와 pi를 가깝게 만들면 된다.
그러면 자연스레 rho의 크기도 1에 가까워질 것이다.
이번엔 확률 분포를 이렇게 바꿔보자.
b
| 1 | 2 | 3 |
|---|---|---|
| 0.2 | 0.2 | 0.6 |


분산이 9.55에서 2.55로, 많이 줄어든 것을 확인할 수 있었다.
이처럼 중요도 샘플링 시 두 확률 분포를 비슷하게 하면 분산을 줄일 수 있다.
단, 강화 학습에서 핵심은 한쪽 정책(확률 분포)은 '탐색'에, 다른 쪽 정책은 '활용'에 이용하는 것이다.
이 조건을 염두에 둔 상태에서 두 확률 분포를 가깝게 조정하면 분산을 줄일 수 있다.
본 내용은 밑바닥부터 시작하는 딥러닝 4를 참고하여 작성되었습니다.
'AI Repository > 기초 강화학습' 카테고리의 다른 글
| [강화학습] 시간차 학습(TD), SARSA, Q-Learning (0) | 2025.09.01 |
|---|---|
| [강화학습] 강화학습에서 최적 정책을 찾는 방법 (0) | 2025.09.01 |
| [강화학습] 벨만 방정식 (0) | 2025.08.29 |
| [강화학습] 마르코프 결정 과정(MDP) (0) | 2025.08.28 |
| [강화학습] 밴디트 문제 (0) | 2025.08.28 |