이번 내용은 지난 장에서 다루지 못했던 "확률적 MDP"의 수식 전개이다.
벨만-포드 알고리즘과 다이나믹 프로그래밍을 만든 수학자 벨만의 또다른 업적, 벨만 방정식에 대해 알아보자.
벨만 방정식은 MDP에서 성립하는 가장 중요한 방정식이며, 많은 강화 학습 알고리즘에 중요한 기초를 제공한다.
사실 순수한 벨만 방정식의 경우, 실용적인 문제에서는 계산량이 너무 많아져서 적용하기 쉽지 않다.
하지만 선형 회귀/로지스틱 회귀에서 딥러닝이 발전했듯이,
벨만 방정식의 도출 과정이 강화학습의 기초(즉, 새로운 기법의 적용 가능성 탐색/연구를 위한 기초)가 되기 때문에, 정확히 인지하고 넘어가는 것이 중요하다.
참고로, 좀 어렵다...
기호가 이것저것 많이 등장해서 읽는데 시간이 좀 걸릴 것이다.
익숙해지는 수밖에 없으니, 반복해서 읽어가며 기호가 좀 잘 읽히게 되는 순간, 이해가 되기 시작할 것이다.
지난 장에서 등장한 기호를 이것 저것 많이 쓰니 아래에 첨부하도록 하겠다.
각 단어에 대한 정의를 명확히 기억하길 바란다.
- MDP
- 결정적
- 확률적
- 마르코프 성질
- MDP의 표현
- 상태 전이(f, p)
- 보상(r)
- 정책(pi, mu)
- 일회성 과제
- 지속적 과제
- 수익(G)
- 할인율(gamma)
- MDP의 가치 함수
- 상태 가치 함수(V_pi, v_pi)
- 최적 가치 함수(v_*)
- 상태 가치 함수(V_pi, v_pi)
- 최적 정책(pi_*)
백업 다이어그램
간단한 예시를 위해 새로운 다이어그램을 소개하겠다.
백업 다이어그램은 '방향 있는 그래프'를 활용하여, '상태, 행동, 보상'의 전이를 표현한 그래프이다.

예시를 그려보면 아래와 같다.
색칠된 노드로 행동을 표현하고, 빈 노드로 상태를 표현한다.
위와 같이 확률적으로 정책이 발생하는 경우, 트리 형태로 상태 변화가 퍼져나갈 수 있다.
이번 장의 목표는 위와 같은 상황에서도 상태 가치 함수를 구하는 것이다.
이때의 핵심이 벨만 방정식이다.
벨만 방정식 도출
확률과 기댓값(사전 준비)
시작하기 전에, 잠시 확률과 기댓값을 복습해보자.
주사위의 각 눈이 나올 확률은 아래와 같이 표현한다.

그럼 이제 주사위를 굴렸을 때 나올 눈의 기댓값을 계산해보자.
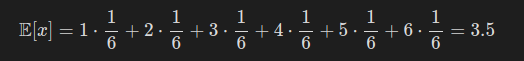
참고로 시그마 기호를 쓰면 다음 식으로도 표현할 수 있다.

그럼 지금부터 살짝 복잡한 문제를 정의해보자.

이번 문제는 주사위를 먼저 던지고 이어서 동전을 던지는 방식으로 진행된다.
이때, 주사위를 던져
- 짝수가 나오면 -> 앞면이 잘 나오는 동전(확률:0.8) 던지기
- 짝수가 나오면 -> 일반 동전(확률:0.5) 던지기
를 수행한다.
이때 앞면이 나와야만 주사위 눈에 적힌 수를 점수로 얻을 수 있다.
x를 주사위 눈이라고 하고, y를 동전을 던진 결과라고 하자.
그렇다면 이렇게 조건부 확률을 정의할 수 있다.

또한 x와 y가 동시에 일어날 확률은 아래와 같다.

이번 문제에서의 보상은 x와 y값에 의해 결정된다. 따라서 보상을 함수 r(x,y)로 나타낼 수 있다.

드디어 우리는 위 문제의 기댓값을 계산할 수 있게 되었다.
이를 수식으로 나타내면 아래와 같다.

이 수식의 형태는 벨만 방정식에서도 동일하게 등장한다.
벨만 방정식 도출
MDP에서 '수익'은 다음과 같이 정의한다.

여기서 t와 t+1 간에 재밌는 관계를 도출할 수 있는데,
먼저 G_t+1 을 살펴보자.
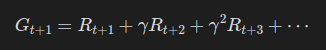
이를 위 식에 대입하면 어떻게 될까?

즉, 점화식 형태가 형성된다!
이 관계는 수많은 강화 학습 이론과 알고리즘에서 사용된다.
이번엔 이걸 상태 가치 함수의 수식과 엮어보자.
상태 가치 함수는 아래와 같이 정의됐다.
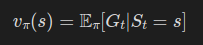
이제 여기에 미래 수익과의 관계를 한번 집어넣어 보자.
위에서 구한 G_t를 대입해보겠다.

이제 마지막 식의 항을 하나씩 구해보자.
가정을 통해 한번 상태 가치 함수를 계산해보자.
좌항의 전개
먼저

부터 시작하겠다.
- 현재 상태는 s이다.
- 에이전트는 정책 pi에 따라 행동한다.
- 다음의 세가지 행동을 취할 수 있다.

에이전트는 이 확률 분포에 따라 행동을 선택한다.
그러면 상태 전이 확률 p에 따라 새로운 상태 s'로 이동한다.
p는 행동 a1을 수행했을 때 다음과 같은 확률을 갖는다.

그리고 마지막으로 보상은 r(s, a, s') 함수로 결정된다
이상이 우리가 처한 상황이다.
이제 예를 들어 계산해보자.
- 에이전트가 0.2의 확률로 행동 a1을 선택하고 0.6의 확률로 상태 s1로 전이한다.
이를 수식으로 표현하면 아래와 같이 된다.
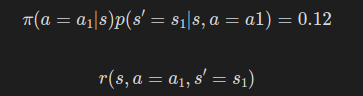
이제 모든 후보에 대해 앞서 주사위와 동전 게임을 수행하며 얻은 수식을 이용하면 기댓값을 계산할 수 있다.
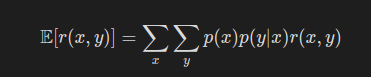
이 수식에서 현재 상태 s 가 조건으로 들어가므로, 이를 적절히 반영하면

이렇게 좌항의 수식을 도출할 수 있었다.
우항의 전개
이제 나머지 우항을 구해보자.

여기서 감마는 할인율, 즉 상수이니 기댓값에 대해서만 다뤄보자.
먼저 상태 가치 함수 표현식에 t+1을 대입해보자.
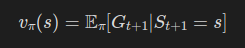
이 식과, 우리가 구하려고 하는 식을 비교해보자.

이 식은 현재 시간이 t일 때 한 단위 뒤 시간의 기대 수익을 의미한다.
문제 해결의 핵심은 조건인 S_t=s를 S_t+1=s로 바꾸는 것이다.
즉, 시간을 한 단위만큼 흘려보내는 것이다.
앞에서와 마찬가지로 구체적인 예를 들어서 설명해보겠다.
지금 에이전트의 상태는 S_t = s이다.
그리고 에이전트가 0.2의 확률로 a1행동을 선택하고, 0.6의 확률로 s_1 상태로 전이한다고 해보자.
그러면

의 확률로
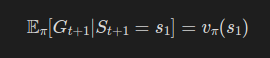
로 전이된다고 할 수 있다.
여기서 해당 '상태'에는 시간의 개념이 들어가 있지 않기 때문에, 다음 단계의 시간을 '보는' 것으로 다음 상태의 가치 함수를 얻을 수 있다.
이렇게 다음 단계의 시간의 상태 가치 함수가, 현재 단계의 '보상'이 된다.
이제 기댓값 E(G_t+1|S_t=s)를 구하려면 모든 후보에 이 계산을 수행하여 다 더하면 된다.

드디어 두 번째 항 전개도 마쳤다.
앞서 전개한 식에 대입하면 다음 식이 도출된다.

이 맨 마지막 변이 바로 벨만 방정식이다.
벨만 방정식은 다음을 표현하는 데 목적을 둔다.
- 상태 s의 상태 가치 함수와
- 다음에 취할 수 있는 상태 s'의 상태 가치 함수 간
- 관계
이는 MDP 내의 모든 상태 s와 모든 정책 pi에 대해 성립한다.
벨만 방정식의 예
정말 어렵게 벨만 방정식에 대한 이해를 마칠 수 있었다.
이제 이걸 써먹어서, '벨만 방정식의 위력'을 느껴보자!
두 칸짜리 그리드 월드

이번에 다룰 문제는 '두 칸짜리 그리드 월드'이다.
- 에이전트는 오른쪽이나 왼쪽으로 이동할 수 있다.
- 상태 전이는 결정적이다.
- 정책은 확률적으로 결정된다.
- 앞장에서는 정책이 결정적으로 정해져 있었고, 각 정책을 평가하는 과정을 수행했었다.
- 에이전트가 L1에서 L2로 이동하면 사과를 받아 +1의 보상을 얻는다.
- 에이전트가 L2에서 L1으로 이동하면 사과가 다시 생성된다.
- 벽에 부딪히면 -1의 보상을 얻는다. 즉, 벌을 받는다.
- 지속적 과제, 즉 '끝이 없는' 문제다.
- 할인율은 0.9로 한다.
먼저 벨만 방정식을 되돌아보자.

여기서 상태 전이는 확률이 아닌 결정적으로 전이되므로, 위 수식에서 p가 f로 바뀌어야 한다.
즉,
- s' = f(s, a)이면 p(s'|s,a)=1
- s' != f(s, a)이면 p(s'|s,a)=0
이다.
이를 위 벨만 방정식에 대입해보면 다음과 같이 정의할 수 있다.

이제 이 식을 이번 문제에 사용해보자.
먼저 상태가 L1일 때 먼저 처리해보겠다.

- 0.5의 확률로 행동 Left를 선택하고 상태는 전이되지 않기
- 보상은 -1
이를 벨만 방정식으로 나타내면 아래와 같다.
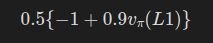
- 0.5의 확률로 행동 Right를 선택하고 L2로 상태 전이하기
- 보상은 1
이를 벨만 방정식으로 나타내면 아래와 같다.

이 두 식을 합쳐서 완전한 벨만 방정식을 구성해보자.

이 식이 상태 L1에서의 벨만 방정식이다.
다음과 같이 정리할 수도 있다.
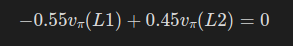
마찬가지로, 상태 L2에서의 벨만 방정식을 구해보자.

이렇게 해서 다음의 연립방정식을 획득할 수 있었다.

이 수식을 풀면 아래와 같아진다.
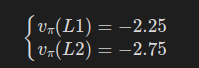
우리는 이렇게 무작위 정책의 상태 가치 함수를 구할 수 있었다.
즉 상태 L1에서 무작위로 행동하면 앞으로 -2.25의 수익을 기대할 수 있고, 상태 L2에서 무작위로 행동하면 -2.75의 수익을 기대할 수 있다는 뜻이다.
벨만 방정식의 의의
지금까지 살펴본 바와 같이 벨만 방정식을 통해 무한히 계속되는 계산을 유한한 연립방정식으로 변환할 수 있었다.
위 값이 말하는 바를 정리하면 아래와 같다.
- v_\pi(L1)=-2.25 는 L1에서 시작해 pi 를 계속 따르면 장기적으로 받는 할인 보상의 기대 총합이 -2.25임
- 값이 음수인 이유: 절반 확률로 양끝에서 벽에 부딪혀 −1 를 자주 맞고, L1→L2 때 받는 +1 보상만으로는 이를 상쇄하지 못함
이번처럼 행동이 무작위로 이루어지더라도 벨만 방정식을 이용하면 상태 가치 함수를 구할 수 있다.
상태 가치 함수는 기대 수익이며 '무한히 이어지는' 보상의 합으로 정의된다.
하지만 위 식에서 보듯 벨만 방정식에는 '무한'이라는 개념이 없다. 벨만 방정식 덕분에 무한의 굴레에서 빠저나온 셈이다.
행동 가치 함수(Q 함수)와 벨만 방정식
행동 가치 함수(action-value function)은 상태 가치 함수 v와 함께 자주 등장하는 함수로,
강화 학습 이론에 단골처럼 등장하는 함수이다.
행동 가치 함수는 관례적으로 Q-함수라고 부르니, 약자 q로 표현하도록 하겠다.
이제 행동 가치 함수를 이용해 벨만 방정식을 도출해보자.
행동 가치 함수
먼저 상태 가치 함수를 복습해보자.

상태 가치 함수의 조건은 아래와 같았다.
- 상태가 s일 것
- 정책이 pi일 것
행동 가치 함수는 여기에 한가지가 더 추가된다.
- 상태가 s일 것
- 정책이 pi일 것
- 행동이 a일 것
이것이 바로 Q 함수이다.

시간 t일 때 상태 s에서 행동 a를 취하고, 시간 t+1 부터는 정책 pi에 따라 행동을 결정한다고 할 때,
이때 얻을 수 있는 기대 수익이 Q 함수인 것이다.
따라서 만약 Q 함수의 행동 a를 정책 pi에 따라 선택하도록 설계하면, Q 함수는 상태 가치 함수와 완전히 동일해진다.
따라서 다음 수식이 성립한다.

행동 가치 함수를 이용한 벨만 방정식
이어서 행동 가치 함수를 이용한 벨만 방정식 도출을 수행해보자.

여기서 상태 s와 행동 a는 정해져 있다. 그렇다면 다음과 같이 식을 전개할 수 있다.

또한, 상태 가치 함수와 행동 가치 함수 간의 관계를 이용하면 다음과 같이도 표현이 가능하다.

위 식이 바로 행동 가치 함수를 이용한 벨만 방정식이다.
벨만 최적 방정식
벨만 방정식은 어떤 정책 pi에 대해 성립하는 방정식이다.
하지만 우리가 궁극적으로 찾으려는 것은 최적 정책이다.
물론 최적 정책도 벨만 방정식을 만족하고, 게다가 정책이 '최적이다'라는 성질을 이용하면 벨만 방정식을 더 간단하게 표현할 수 있다.
상태 가치 함수의 벨만 최적 방정식
먼저 상태 가치 함수로 표현한 벨만 방정식을 보자.

이 식이 바로 상태 가치 함수의 벨만 최적 방정식이다.

이 식에는 이러한 원리가 적용된다.
- 최적 정책은 항상 최선의 행동을 고른다.
- 따라서 확률적 정책은 결정적 정책으로 치환이 가능해진다.
- 따라서 정책함수 pi는 최대를 만드는 행동 a만 선택한다.
- 따라서 시그마가 max 함수로 바뀐다.
행동 가치 함수의 벨만 최적 방정식
행동 가치 함수의 벨만 최적 방정식은 최적 행동 가치 함수라고도 불린다.
앞서 상태 가치 함수와 유사하게 벨만 최적 방정식을 유도하면 다음과 같이 치환이 가능해진다.
이번에도 비교를 위해 행동 가치 함수의 벨만 방정식을 보자.
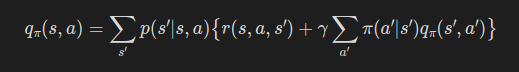
아래 식이 바로 행동 가치 함수로 표현한 벨만 최적 방정식이다.
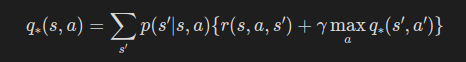
이번에도 벨만 방정식의 정책 함수 sum 부분이 max_a로 대체되었다.
벨만 최적 방정식의 예
이제 이 벨만 최적 방정식을 사용해보자.
앞서 설명했던 '두 칸짜리 그리드 월드'를 다시 한번 다뤄보자.

- 에이전트는 오른쪽이나 왼쪽으로 이동할 수 있다.
- 상태 전이는 결정적이다.
- 정책은 확률적으로 결정된다.
- 에이전트가 L1에서 L2로 이동하면 사과를 받아 +1의 보상을 얻는다.
- 에이전트가 L2에서 L1으로 이동하면 사과가 다시 생성된다.
- 벽에 부딪히면 -1의 보상을 얻는다. 즉, 벌을 받는다.
- 지속적 과제, 즉 '끝이 없는' 문제다.
- 할인율은 0.9로 한다.
벨만 최적 방정식 적용
먼저 벨만 최적 방정식을 다시 보자.
상태 가치 함수로 표현하도록 하겠다.

또한 상태 전이가 결정적이라면 다음과 같이 단순화할 수 있다.

이렇게 단순화할 수 있는 이유는 다음 식이 성립하기 때문이다.
- s' = f(s, a)이면 p(s'|s,a)=1
- s' != f(s, a)이면 p(s'|s,a)=0
따라서 할인율이 0.9일 때의 벨만 최적 방정식을 다음과 같이 구할 수 있다.

두 칸 짜리 그리드 월드처럼 단순한 문제라면 벨만 최적 방정식을 직접 손으로 계산하여 풀 수도 있다.
하지만 우리가 알고 싶은 것은 '최적 정책'이다.
바로 이어서 최적 정책에 대해 알아보자.
최적 정책 구하기
최적 행동 가치 함수 q*를 알고 있다고 가정하자.
그렇다면 상태 s에서의 최적 행동은 다음과 같이 구할 수 있다.

argmax 는 최댓값이 아니라, '최댓값을 만들어내는 인수' (여기선 행동 a)를 반환한다.
즉, 행동 가치를 가장 높이는 '최적 행동' a를 찾아 반환한다는 뜻이다.
이 자체로는 큰 의미가 없어보인다.
다른 식과 본격적으로 결합해보자.

이 행동 가치 함수로 표현한 벨만 방정식을 최적 행동 함수 mu*에 결합해보자.
그러면 아래 식이 만들어진다.

이와 같이 최적 상태 가치 함수 v*를 이용해 최적 정책 mu*를 구할 수 있게 되었다.
그럼 이제 이 argmax를 찾아보자.
먼저 상태 L1일때를 살펴보자.
행동 Left를 선택할 경우, 최적 행동 가치 함수는 다음과 같은 결과를 출력한다.

또한 행동 Right를 선택할 경우, 최적 행동 가치 함수는 다음과 같은 결과를 출력한다.

행동 Right가 행동 Left보다 더 높은 결과를 낸 것을 확인할 수 있었다.
따라서 L1에서의 최적 정책은 Right 행동이다.
이와 같은 방식으로 L2에서 또한 구할 수 있다.
정리
이번 장에서 배운 내용들을 키워드로 정리해보자.
- MDP
- 상태 가치 함수(v)
- 행동 가치 함수(Q 함수)
- 벨만 방정식
- 상태 가치 함수 벨만 방정식
- 행동 가치 함수 벨만 방정식(최적 행동 가치 함수)
- 벨만 방정식을 이용한 연립 방정식의 해
- 벨만 방정식의 의의
- 벨만 방정식을 이용한 서로 다른 수익 간의 관계
벨만 방정식

벨만 최적 방정식

최적 정책

'AI Repository > 기초 강화학습' 카테고리의 다른 글
| [강화학습] 강화학습에서 최적 정책을 찾는 방법 (0) | 2025.09.01 |
|---|---|
| [강화학습] Off-Policy, On-Policy, 중요도 샘플링 (0) | 2025.08.31 |
| [강화학습] 마르코프 결정 과정(MDP) (0) | 2025.08.28 |
| [강화학습] 밴디트 문제 (0) | 2025.08.28 |
| Define-by-Run과 Define-and-Run (0) | 2025.08.25 |