추천 시스템과 같은 문제에서 밴디트 문제는 가장 간단한 예시로 등장한다.
강화학습의 기초를 닦기 위해, 밴디트 문제에 대해 이해해보고, 그 해법을 공부해보자.
머신러닝 분류와 강화학습
머신러닝 기법들은 다루는 문제의 성격을 기준으로 분류할 수 있다.
그리고 크게 다음 세가지로 나뉜다.
- 지도 학습
- 비지도 학습
- 강화 학습
지도 학습
지도학습은 머신러닝에서 가장 전통적인 기법으로, 입력(문제)과 출력(정답)을 쌍으로 묶은 데이터를 통해 문제를 해결한다.
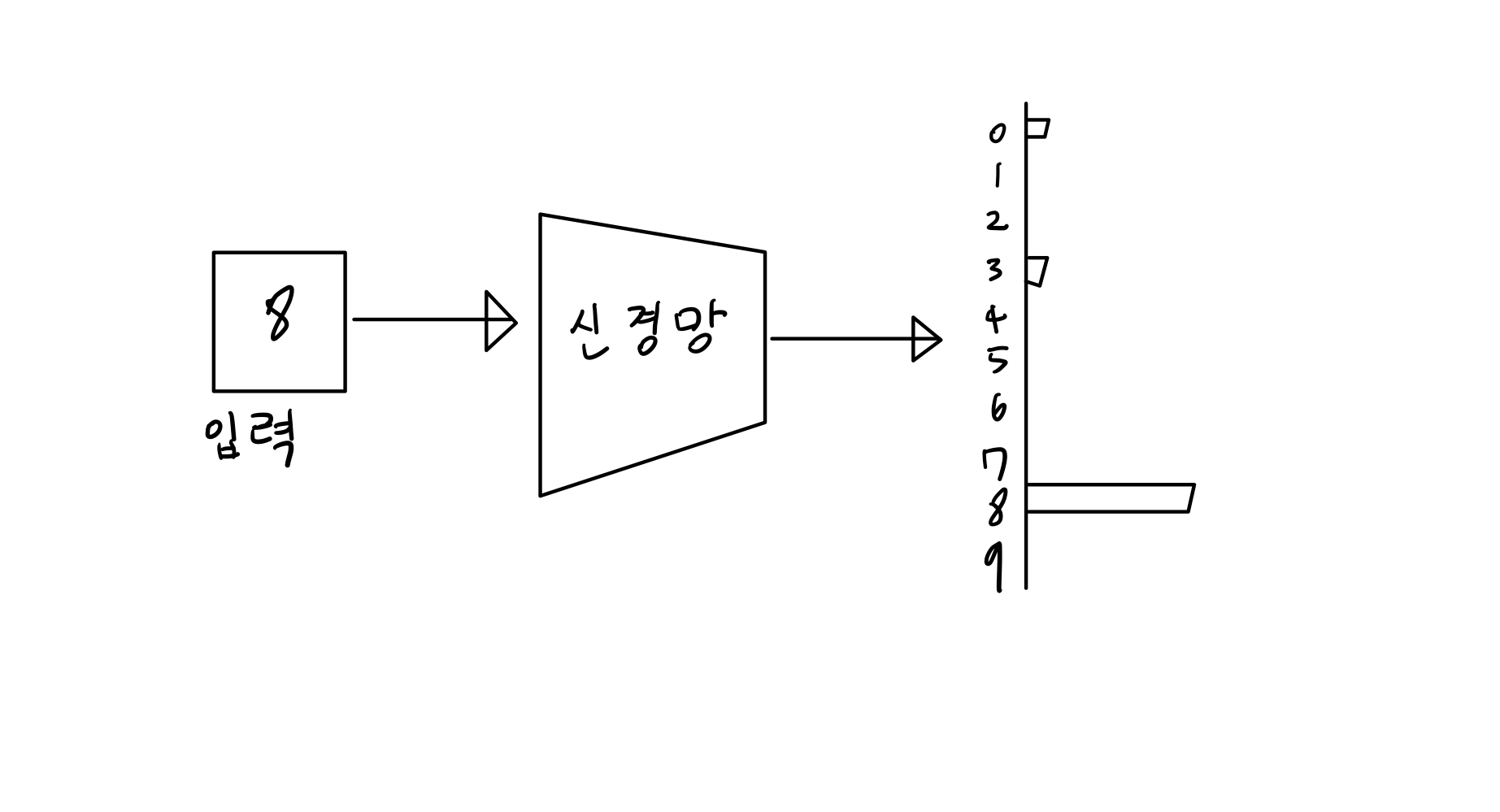
지도학습의 가장 큰 특징으로는 이와 같은 명확한 '정답 레이블'의 존재를 들 수 있다.
비지도 학습

비지도 학습에서는 이러한 '정답 레이블'이 존재하지 않는다.
비지도 학습은 데이터에 숨어있는 구조나 패턴을 찾는 용도로 쓰이며, 아래와 같은 곳에 활용된다.
- 군집화(클러스터링)
- 특성 추출
- 차원 축소
비지도 학습의 경우 정답 레이블이 필요하지 않기 때문에, 빅데이터라 할지라도 준비하기가 비교적 쉬운 장점이 존재한다.
강화 학습
강화학습은 지도 학습이나 비지도 학습과는 다른 유형의 문제를 다룬다.
강화학습에서는 에이전트와 환경이 서로 상호작용한다.

- 에이전트
- 행동 주체
- 환경의 상태를 관찰하고,
- 상태에 적합한 행동을 수행한다.
- 또한 환경으로부터 보상을 제공받는다.
- 환경
- 상태를 갖고,
- 에이전트의 행동에 맞춰 변화한다.
- 에이전트에게 적절한 보상을 지급한다.
- 강화학습의 목표는 에이전트가 얻는 보상의 총합을 극대화하는 것이다.
강화 학습에서는 환경의 피드백으로 '보상'을 받는데, 이는 지도학습에서 말하는 정답 레이블과는 성격이 다르다.
보상은 행동에 대한 피드백일 뿐, 그 보상으로부터 지금까지 취한 행동이 최적인지 여부는 판단할 수 없다.
반면, 지도 학습에서는 '정답'이 제공된다. 이 정답과의 오차를 손실 함수를 통해 평가를 수행할 수 있다.
밴디트 문제
이제부터 강화학습에서 다루는 구체적인 문제를 살펴보자.
그럼 처음이니 가장 간단한 문제에 속하는 밴디트 문제에 대해 알아보자.
밴디트 문제란?
밴딧(bandit)은 '슬롯머신'의 또 다른 이름이다.
여기서 말하는 슬롯머신은
- 손잡이가 있고,
- 손잡이를 당기면
- 그림들이 한꺼번에 바뀐다.
- 바뀐 그림들의 조합에 따라 코인의 액수가 정해진다.
밴디트의 원래 의미는 '도적' 혹은 '산적' 이다.
그런데 언제부턴가 도박꾼들 사이에서 슬롯머신을 '외팔이 도적'(one-armed bandit)이라고 부른데에서 이러한 의미가 부여되었다.
이는 슬롯머신의 손잡이가 하나(외팔이)이고, 대부분 돈을 잃게 되므로 '도적'이라 부르게 되었다고 한다.
밴디트 문제를 정확하게는 멀티-암드 밴딧 문제 라고 한다.
정확히는 아래와 같이 슬롯 머신이 여러대인 문제를 생각하면 된다.

밴디트 문제에서는 슬롯머신 각각의 특성이 서로 다르다.
이 상황에서 플레이어는 각 슬롯머신에 대한 정보를 모르며, 정해진 횟수(예: 1000회)만 플레이가 가능하다.
그러므로 플레이어는 승률이 좋은 특성을 갖는 하나의 슬롯머신을 찾고, 그 기계를 통해 정해진 횟수 안에 코인을 최대한 많이 얻는 것이 목표이다.
밴딧 문제를 강화학습으로 표현하면?
- 환경
- 슬롯머신
- 에이전트
- 플레이어
- 행동
- 플레이어가 슬롯머신 중 한 대를 선택해 플레이
- 보상
- 슬롯머신에서 얻는 코인
일반적인 강화학습 문제에서 환경에는 상태 정보가 있다.
그런데 이 밴딧 문제에서는 상태 정보가 없다.
상태가 변하는 문제는 마르코프 결정 과정에서 다룰 것이다.
좋은 슬롯머신이란?
그럼 '좋은 슬롯머신'을 어떻게 수학적으로 정의할 수 있을까?
잠시 통계 지식을 끌고 와보자.
슬롯머신과 같은 문제는 확률에 의해 보상이 결정된다.
그 안에서 우리는 기댓값으로 각 슬롯머신의 가치를 평가할 수 있다.
수식으로 표현하기
그럼 이제 이를 수식으로 표현하기 위해 몇가지 정의를 익혀두자.
확률변수
슬롯머신은 보상 R(eward)를 일정 확률로 지급한다.
이와 같이 얻는 값이 확률적으로 결정되는 변수를 확률 변수라고 한다.
앞의 예시에선 보상 = 확률 변수라고 할 수 있는 것이다.
기댓값과 행동 가치
기댓값은 Expectation의 머릿글자를 따라 E를 쓴다.
예를 들어, 보상 R의 기댓값은 아래와 같이 표현 가능하다.

또한, 행동 A를 했을 때의 보상 기댓값은 아래와 같이 표기한다.

보상에 대한 기댓값을 행동 가치라고 하며, 강화학습에서는 관례적으로 행동 가치를 Q 또는 q로 표기한다.

위 수식은 행동 A에 대한 행동 가치 q를 나타낸다.
- 소문자 q는 '실제 행동 가치'를 나타내고,
- 대문자 Q는 '추정 행동 가치'를 나타낸다.
- 에이전트는 일반적으로 실제 행동 가치 q를 알 수 없기 때문에, 추정치 Q를 사용한다.
이제 본격적으로 밴디트 알고리즘에 대해 알아보자.
밴디트 알고리즘
지금까지의 내용을 간단하게 정리해보자.
- 만약 각 슬롯머신의 가치(보상 기댓값)를 알면 플레이어는 가장 좋은 슬롯머신을 고를 수 있다.
- 그러나 플레이어는 각 슬롯머신의 가치를 알 수 없다.
- 따라서 플레이어는 각 슬롯머신의 가치를 (가능한 한 정확하게) 추정해야 한다.
이제 이 슬롯머신의 가치를 추정하는 방법을 알아보자.
가치 추정 방법
플레이어가 슬롯머신 a와 b를 각각 세번씩 플레이하여, 아래와 같은 보상을 얻었다고 하자.
| 슬롯머신 | 첫 번째 | 두 번째 | 세 번째 |
|---|---|---|---|
| a | 0 | 1 | 5 |
| b | 1 | 0 | 0 |
플레이어는 슬롯머신 a와 b를 각각 세번씩 플레이했다.
이 결과로부터 추정치를 아래와 같이 추정할 수 있다.

이어서 슬롯머신의 가치를 추정하는 걸 코드로 작성해보자.
평균을 구하는 코드
평균은 다음과 같이 정의 가능하다.

각 횟수의 가중치를 1로 둔 가중평균을 구했다.


매 반복마다 평가치의 변화를 계산하면 이렇게 변화하는데, 계산식이 좀 비효율적인 느낌이 들지 않는가?
이번엔 점화식을 이용해 조금 수식을 변형해보자.

이전 상태를 이용해 R_n에 간단한 값을 더해 현재의 Qn을 구할 수 있게 되었다!
여기서 한번만 더 최적화해보자.
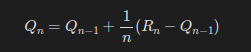
이로써 점화식을 이용해 연산을 최적화하면서, 코드로 작성하기도 쉬운 형태가 되었다.
여기 수식에서 한가지 인사이트를 얻어가 보자.
- Q_n-1 이 Q_n으로 갱신될 때, R_n - Q_n-1 의 길이에 1/n을 곱한 값만큼 이동한다.
- 이때 Rn방향으로 얼마나 진행되느냐는 1/n 값이 결정한다.
- 이처럼 1/n은 갱신되는 양을 조정하기 때문에 학습률(learning rate)이라고 한다.
즉, n이 커질수록 Qn은 점차 갱신되기 어려워진다.
이상을 바탕으로 코드로 구현하면 아래와 같다.

이런 식으로 표본평균을 증가시키며 구하는 것을 incremental implementation 이라고 한다.
플레이어의 정책
이제 플레이어(에이전트)가 어떤 전략을 취해야 하는지에 대해 생각해보자.
아마 가장 직관적인 정책은 "실제로 플레이하고 결과가 가장 좋은 슬롯머신을 선택"하는 것일 것이다.
아마 알고리즘을 구현한다면 아래와 같을 것이다.
- 모든 슬롯머신을 각각 한번씩 플레이해 그 행동 가치를 힙에 넣는다.
- 매 수행마다 힙에서 행동 가치가 가장 높은 슬롯머신을 하나 꺼내, 1회 수행 뒤 갱신하여 힙에 다시 넣는다.
- 이를 정해진 횟수까지 반복한다.
이러한 정책을 탐욕 정책(greedy policy라고 한다.)
탐욕 정책은 좋아 보이지만 문제도 있다.
슬롯머신의 가치 추정치에 '불확실성'이 스며 있기 때문에, 최고의 슬롯머신에서 안좋은 결과가 나와 힙의 하위에 계속 쳐박혀있을 수도 있다.
즉, 확실하지 않은 추정치를 전적으로 신뢰하면 최선의 행동을 놓칠 수 있다.
여기까지 생각이 닿으면 플레이어에게 다음의 두가지 행동을 요구하게 된다.
- 활용(exploitation): 지금까지 실제로 플레이한 결과를 바탕으로 가장 좋다고 생각되는 슬롯머신을 플레이
- 탐색(exploration): 슬롯머신의 가치를 정확하게 추정하기 위해 다양한 슬롯머신을 시도
이 두 행동은 서로 상충관계이다. 즉 하나를 시도하면, 다른 하나를 수행하지 못하게 된다.
결국 강화학습 알고리즘은 '활용과 탐색의 균형'을 어떻게 잡느냐의 문제로 귀결된다.
간단한 것부터 복잡한 것까지 정말 많지만 그중에서도 가장 기본적이고 응용하기 좋은 알고리즘은 입실론-탐욕 정책(입실론-그리디 정책)이다.
입실론-그리디 정책
소제목으로 빼뒀지만 사실 별 거 아닌데, 아래와 같은 방식으로 동작한다.
- 입실론=0.1의 확률로 '탐색'을 수행
- 나머지 (1-0.1=0.9)의 확률로 '활용'을 수행
한번 이 정책을 파이썬으로 구현해보자.
밴디트 알고리즘 구현
구현하기 전에, 조건을 단순화하여 슬롯머신이 반환하는 코인을 최대 1개로 제한하겠다.
이러면 승률이 그대로 슬롯머신의 가치가 되는 것이다.
슬롯머신 구현

간단하게 랜덤한 확률을 갖는 슬롯머신을 구현했다.
이제 이 밴딧 객체를 가지고 슬롯머신 놀이를 해보자.
에이전트 구현
먼저 간단하게 10개 중 랜덤한 슬롯머신을 골라 실행하는 코드를 작성해보자.
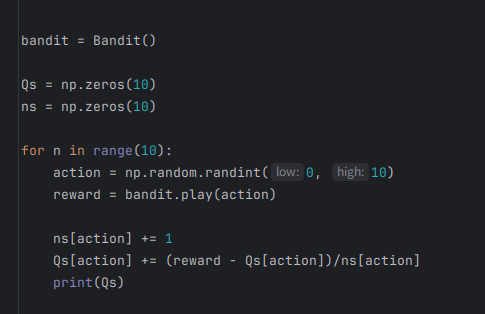
- Qs: 각 슬롯머신의 행동 가치 10개를 저장한 넘파이 배열
- ns: 각 슬롯머신의 실행 횟수
이러한 형식에 맞춰 에이전트를 구현해보자.

- 초기화 매개변수 epsilon을 통해 입실론 값을 지정하고, 그 값에 따라 get_action에서 행동 양식을 결정한다.
- np.argmax(self.Qs)를 통해 가장 행동 가치가 큰 슬롯 머신을 가져와 행동을 수행한다.
실행해보기
이제 Bandit 클래스와 Agent 클래스를 이용하여 행동을 취해보자.


이 결과를 봤을 때, 최종적으로 1000번 중 800번정도 승리했다는 사실을 알 수 있었다.
그래프에서 볼 수 있듯이, 단계가 늘어날 때마다 보상의 총합이 꾸준히 증가한다.
다만, 증가 방식의 특징, 단계 증가와 보상 증가의 정밀한 관계같은 것은 이 그래프로 알아내기 어렵기 때문에, 단계별 승률을 그래프로 다시 뿌려보자.

단계가 올라갈수록 승률이 상승하는 것을 확인할 수 있었다.
알고리즘의 평균적인 특성
하지만 이 강화학습 문제는 결과가 실험 때마다 달라지는 문제가 있다.
강화 학습 알고리즘을 비교할 때 (대부분의 경우) 무작위성 때문에 한 번의 실험만으로 판단하는 건 큰 의미가 없다.
그보다는 알고리즘의 '평균적인 우수성'을 평가해야 한다.
그래서 슬롯머신을 1000번 플레이하는 실험을 총 200번 반복하여 평균을 내보겠다.
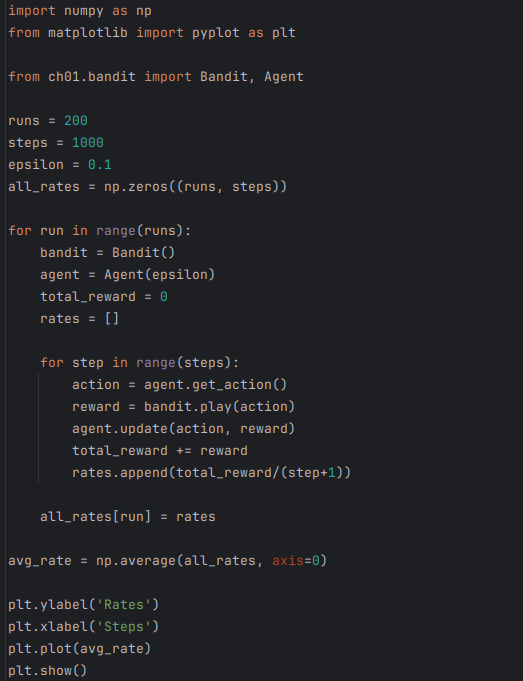
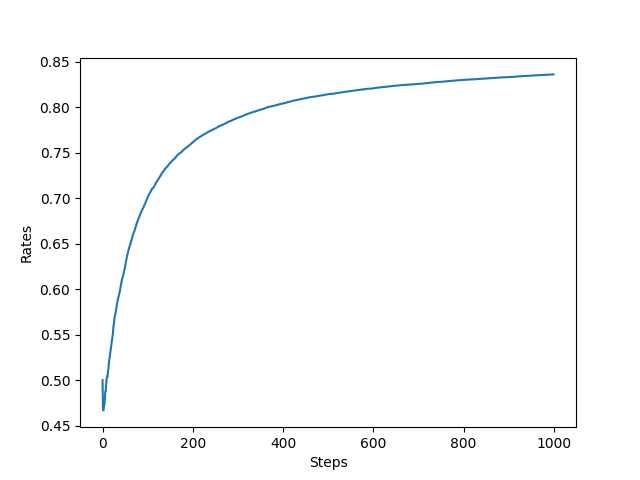
훨씬 성능이 가시적으로 보이고 있다.
알고리즘을 평가할 때는 이처럼 평균을 잘 이용해야 한다.
승률이 처음에는 0.5 정도로 시작해서 500단계 정도에 이르러 거의 최대를 찍는다.
비교군으로 epsilon을 바꿔 다시 테스트해보자.
먼저 입실론을 0.01로 설정했을 때였다.

탐색의 비율이 지나치게 적어 승률이 잘 오르지 않는 것을 알 수 있었다.
이번엔 입실론을 0.3으로 맞춰보자.

이 경우 입실론이 지나치게 커, '활용'을 선택하는 비율이 너무 낮아 성능이 최대까지 올라가지 않는 것을 확인할 수 있었다.
이와 같이 '활용과 탐색의 균형'을 조절해야 좋은 구현을 발견할 수 있다.
비정상 문제
지금까지 다룬 '밴디트 문제'는 분류상 정상 문제(Stationary problem)에 속한다.
정상 문제(Stationary Problem)
- 보상의 확률 분포가 변하지 않는 문제
- 밴딧 문제에서 슬롯머신에 설정된 승률은 줄곧 고정된 채였다.
그렇다면 슬롯머신에 설정된 승률이 매번 바뀌면 어떻게 될까?
비정상 문제(Non-stationary Problem)
아래 코드를 살펴보자.

이번엔 self.rates에 작은 노이즈를 추가했다.
이는 평균이 0, 표준편차가 1인 정규분포*0.1를 작은 노이즈로 추가시켰다.
이처럼 보상의 확률 분포가 변하도록 설정된 문제를 비정상 문제라고 한다.
그럼 이런 문제는 어떻게 푸는게 좋을까?
비정상 문제를 풀기 위해서
잠깐 기억을 되살려 행동 가치를 결정하는 수식을 떠올려보자.
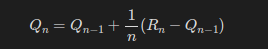
우리는 수식을 이런 식으로 세워두었는데, 여기에 한가지 함정이 있다.
n이 커질수록 Qn은 점차 갱신되기 어려워진다.
현재 횟수가 커질수록 과거의 행동가치는 의미가 없어진다. (더 많이 변화했을 가능성이 높기 때문)
반대로 새로 얻은 보상의 가중치는 점점 거쳐야 한다.(비교적 최신 데이터)
그래서, 가중치인 1/n을 a(알파)라는 고정값으로 바꾼다.(0<a<1)
이렇게 수식을 바꾸면 아래와 같다.

위에서 잠깐 언급했는데, 정상 문제를 위한 행동 가치 수식은 모든 보상의 가중치가 1인 가중 평균이었다.
이런 식으로 행동 가치 수식을 변경하면, 각 보상의 가중치는 어떻게 될까?
위 식을 전개해보자.
$$Q_n = \alpha R_n + \alpha(1-\alpha)R_{n-1} + \cdots + \alpha(1-\alpha)^{n-1}R_1 + (1-\alpha)^nQ_0$$
위 식에서 각 보상의 가중치가 기하급수적으로 감소함을 알 수 있다.
- R_n 의 가중치 = alpha
- R_n-1의 가중치 = alpha(1-alpha)
- R_n-2의 가중치 = alpha(1-alpha)^2
- ...
그래서 아래 식을 지수 이동 평균(exponential moving average)라고 한다.
$$Q_n = Q_{n-1} + \alpha(R_n - Q_{n-1})$$
Gradient 최적화 방법 중 Adam에서 비슷한 수식을 본 기억이 있을 것이다.
여기서 사용한 수식도 지수 이동 평균이다.
비정상 문제 풀기
이제 비정상 밴디트 문제를 실제로 풀어보자.
먼저 에이전트를 아래와 같이 구현했다.

그리고 실행 코드는 아래와 같이 설정했다.

alpha값은 0.8로 지정했다.
그 결과는 아래와 같다.
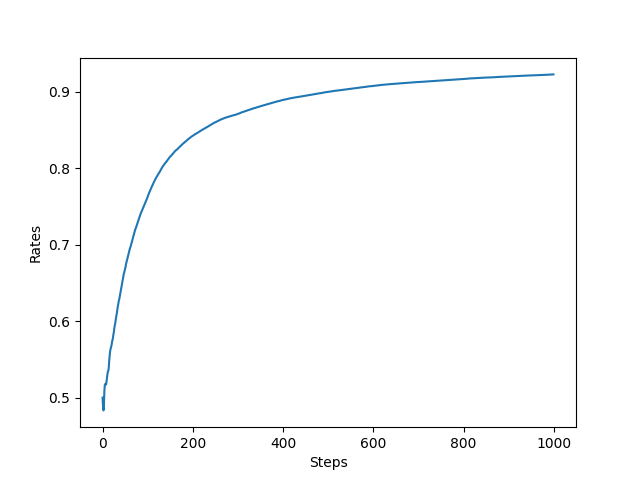
잠깐 일반 Agent를 사용했을 때와 비교해보자.
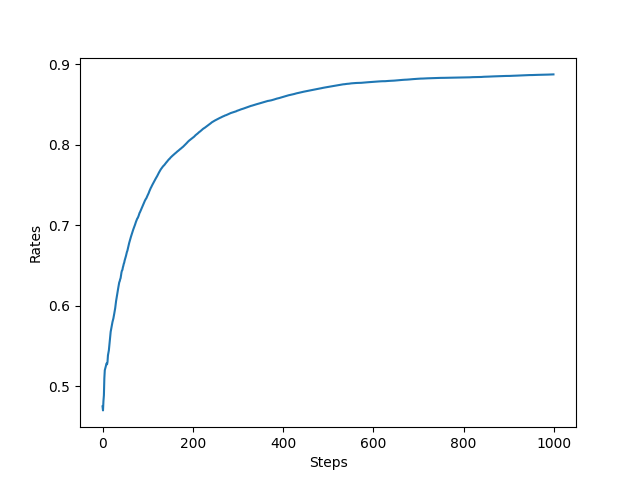
둘을 비교해보면 시간이 지날수록 고정값 알파로 갱신할 때의 효과가 더 좋아짐을 알 수 있었다.
이를 통해 비정상 문제에서는 고정값 알파로 갱신하는 방식이 적합하다는 사실을 알 수 있다.
본 내용은 밑바닥부터 시작하는 딥러닝 4를 참고하여 작성되었습니다.
밑바닥부터 시작하는 딥러닝 4 - 예스24
『밑바닥부터 시작하는 딥러닝』 시리즈, 이번엔 강화 학습이다! 강화 학습 핵심 이론부터 문제 풀이, 심층 강화 학습까지 한 권에!이 책의 특징은 제목 그대로 ‘밑바닥부터 만들어가는 것’이
www.yes24.com
'AI Repository > 기초 강화학습' 카테고리의 다른 글
| [강화학습] 벨만 방정식 (0) | 2025.08.29 |
|---|---|
| [강화학습] 마르코프 결정 과정(MDP) (0) | 2025.08.28 |
| Define-by-Run과 Define-and-Run (0) | 2025.08.25 |
| python - from A import B와 import A.B as b의 차이 (0) | 2025.08.25 |
| python 애스터리스크(*) - 언패킹의 역할과 예제 (0) | 2025.08.25 |