사실 '다이나믹'도 아니고, '프로그래밍'도 아닌 다이나믹 프로그래밍은 알고리즘 문제의 단골 요소이자 매우 효율적인 컴퓨터공학의 계산 효율화 방법이다.
DP는 벨만-포드 알고리즘과 벨만 방정식, 강화학습의 토대를 마련한 미국의 응용수학자 리처드 E. 벨만이 발견했다.
이는 리액트의 렌더링 및 BFS, 캐싱, 비즈니스 로직 및 게임 엔진 최적화부터 심지어는 RL에까지 등장하고 있다.
이 DP에 대해, 지금부터 차근차근 알아보자.
DP의 성질은 딱 두가지로 정리가 가능하다
- 최적 부분구조
- 중복 부분문제
최적 부분구조
최적 부분구조(Optimal Substructure)은 "경로에 관계없이" 다음 문제의 해답이 이전 부분문제의 최적화로 구해지는 구조를 의미한다.
이를 다르게 표현하면, 뒷 문제의 정답을 구하는 과정이 앞 문제의 정답을 구하는 과정에 독립적이라고 표현할 수 있다.
이는 현재 상태가 과거의 상태와 연관이 없어야 DP의 적용이 가능해진다는 의미이기도 하다.
중복 부분문제
중복 부분문제(Overlapping Subproblem)는 특정 주어진 부분문제가 여러 상위 문제의 하위 부분문제로 이용됨을 의미한다.
이는 같은 문제가 여러번 반복되기에, 이를 "기억해 두면" 계산적으로 효율성을 챙길 수 있음을 의미한다.
중복 부분문제의 '중복성'과, 최적 부분구조의 '독립성'이 만나면 탁월한 효과를 낼 수 있게 된다.
메모이제이션
그렇게 정의된 DP는, 메모이제이션(memoization)이라는 기법을 통해 최적화가 이루어지게 된다.
- 각 부분문제는 한번만 풀어야 한다.
- 같은 부분문제는 구할 때 마다 정답이 같다.
- 따라서, 정답을 한번 구했으면, 정답을 어딘가에 메모해둔다.
이를 통해 중복된 계산을 건너뛰고, 계산복잡도를 낮출 수 있게 된다.
귀납법(강귀납법)
이는 수학적 개념 한가지와 연결되는데, 그 대상은 바로 수학적 귀납법이다.
DP로 문제를 풀려면 수학적 귀납법을 위한 점화식이 필요해지게 된다.
이는 실제 DP로 문제를 풀 때 가장 확실하게 드러난다.

이를 통해 DP가 성립하기 위한 기본 구조를 다음과 같이 정의할 수 있다.
- P(1)이 성립해야 한다.
- P(n)이 성립하면 P(n+1)이 성립해야 한다.
즉, DP는 다음 두가지를 만족해야 한다.
- 현재 규칙이 초기조건으로 수렴할 수 있어야 한다.
- DP[i-k]가 왜 참인가?
- 초기조건으로 귀납적으로 도달할 수 있는가?
- DP[i] 에서 어떻게 "이전"으로 되돌아갈 수 있는가?
- DP[i]를 DP[i-k]로 표현한 식을 세울 수 있는가?
- DP[i-k]가 왜 참인가?
- 수렴한 초기 조건이 참이어야 한다.
DP는 왜 어려운가?
DP가 어려운데에는, 식의 수학적 정의라는, 이 정의의 난이도에 있다.
일반적으로 DP문제는 DP라는 것을 파악하기 어려운데, 이는 DP의 정의 과정이 그 자체로 다음 세가지의 지정을 요구하기 때문이다.
- 우리가 마음대로 조정할 수 있는 독립변수는 무엇인가?
- 이 독립변수에 영향을 받는 우리가 구하고자 하는 종속변수는 무엇인가?
- 종속변수에 영향을 끼치지만 우리가 조절할 수 없는 상수는 무엇인가?
즉, DP는 '어느것이 독립변수이고, 어느것이 종속변수인지' 명확히 해야, 효율적인 DP 계산을 유도해낼 수 있다.
- 만약 종속변수를 독립변수로 오인하면, 쓸데없는 차원이 하나 늘어나 DP의 계산에 비효율이 발생한다.
- 만약 독립변수를 종속변수로 오인하면, 답이 제대로 나오지 않는 문제가 발생한다.
부족하지만, 여기에 몇가지 팁을 얹어보겠다.
- y = f(x1, x2) + C 형태로 수식을 정의해보자.
- 이러면 독립변수와 종속변수, 그리고 고정해둬야 하는 상수가 한눈에 보인다.
- 현재 상태를 결정하는 독립변수의 개수를 이용해 DP의 차원을 결정하는 것이 좋다.

- 부분 문제를 그래프로 표현하다 보면, 숨겨진 독립변수와 결정되는 종속변수를 파악할 수 있다.
DP의 시간복잡도
DP의 시간복잡도는 다음과 같이 정의된다.

예제 - "Frog 1" (Easy)
https://atcoder.jp/contests/dp/tasks/dp_a
A - Frog 1
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
문제는 개구리가 돌 1에서 돌 N(N <= 10^5)까지 이동하는 데 필요한 최소 총 비용을 구하는 것이다.
개구리는 한 번에 1칸 또는 2칸만 뛸 수 있다.
두 돌 i와 j 사이를 이동하는 비용은 |h_i - h_j|로 주어지며, 여기서 h_i는 돌 i의 높이를 의미한다.
가볍게 한번 풀어보자.
동적 프로그래밍 없이 풀기
시간 복잡도: O(2^N)
개구리는 매번 두 가지 선택지가 있으므로, 재귀 호출을 이용해 “1칸을 뛸 경우”와 “2칸을 뛸 경우”를 모두 계산할 수 있다.
이렇게 하면 각 단계마다 왼쪽, 오른쪽 서브트리로 분기되며, 점프가 하나 추가될 때마다 경우의 수가 두 배가 되므로 시간 복잡도가 지수적으로 증가하게 된다.
그러나 동적 프로그래밍(DP)을 사용하면 “최적 상태”를 기록해 두어 중복 계산을 피할 수 있다. 예를 들어, 점프 순서가 1,2,1이든 2,1,2이든 결국 돌 3에서의 상태를 다시 계산해야 하는데, DP는 이런 상태를 캐싱하여 재활용할 수 있게 해준다.
동적 프로그래밍을 사용한 풀이
시간 복잡도: O(N)
동적 프로그래밍의 형태는 크게 아래와 같은 두가지 형태가 있다.
- 탑다운 DP
- 바텀업 DP
여기서는 바텀업 DP에 집중하여 설명을 진행해보겠다.
그리고 바텀업 DP에는 다음 두가지 주요 접근 방식이 있다.
- Push DP: 현재 상태를 기준으로 미래 상태를 업데이트한다.
- Pull DP: 현재 상태를 과거 상태로부터 계산한다.
아래에서 두 가지 방식을 모두 다룰 것이다.
실제 문제를 풀 때는 이 두가지 방식이 모두 접근 가능하므로,
현재 문제를 설명하는데 잘 맞는다고 생각하는 접근 방식을 채택하여 사용하자.
(하위에서 상위를 도출하는 느낌인지, 상위에서 하위로 수렴하는 개념인지)
Push DP
개구리가 할 수 있는 선택지는 오직 두 가지이다
- i+1로 1칸 점프
- i+2로 2칸 점프
dp[i]를 “돌 i에 도착하는 데 필요한 최소 비용”이라고 정의하면, 점화식은 다음과 같다.
- 돌 i+1로 1칸 점프

- 돌 i+2로 2칸 점프

초기 조건으로 dp[0] = 0 (개구리가 이미 첫 번째 돌에 있음)에서 시작하여 dp[1],dp[2], ..., dp[N - 1]을 계산하는 코드는 다음과 같다.
package gold.introductiontodp;
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
import static java.lang.Math.abs;
public class Frog1 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n];
StringTokenizer stringTokenizer = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(stringTokenizer.nextToken());
}
int[] dp = new int[n];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int i = 0; i < n; i++) {
if (i + 1 < n) {
int one = abs(arr[i] - arr[i + 1]);
dp[i + 1] = Math.min(dp[i + 1], dp[i] + one);
}
if (i + 2 < n) {
int two = abs(arr[i] - arr[i + 2]);
dp[i + 2] = Math.min(dp[i + 2], dp[i] + two);
}
}
pw.println(dp[n - 1]);
br.close();
pw.close();
}
}Pull DP
개구리가 할 수 있는 선택지는 오직 두 가지이다
- i-1에서 1칸 점프
- i-2에서 2칸 점프
- 돌 i - 1에서 점프

- i - 2에서 점프

초기 조건으로 dp[0] = 0에서 시작하여 dp[1], dp[2], ..., dp[N - 1]을 계산할 것이다.
package gold.introductiontodp;
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
import static java.lang.Math.abs;
public class Frog1 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n];
StringTokenizer stringTokenizer = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(stringTokenizer.nextToken());
}
int[] dp = new int[n];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int i = 0; i < n; i++) {
if (i - 1 >= 0) {
int one = abs(arr[i] - arr[i - 1]);
dp[i] = Math.min(dp[i], dp[i - 1] + one);
}
if (i - 2 >= 0) {
int two = abs(arr[i] - arr[i - 2]);
dp[i] = Math.min(dp[i], dp[i - 2] + two);
}
}
pw.println(dp[n - 1]);
br.close();
pw.close();
}
}대표적인 DP 점화식 유형
이 내용은 다른 글들을 통해 차근차근 하나씩 설명할 예정이다.
일단 이런 점화식 내용이 있다는 것을 알아만 두자.
상수항 DP

카데인 & LIS

배낭 문제 DP
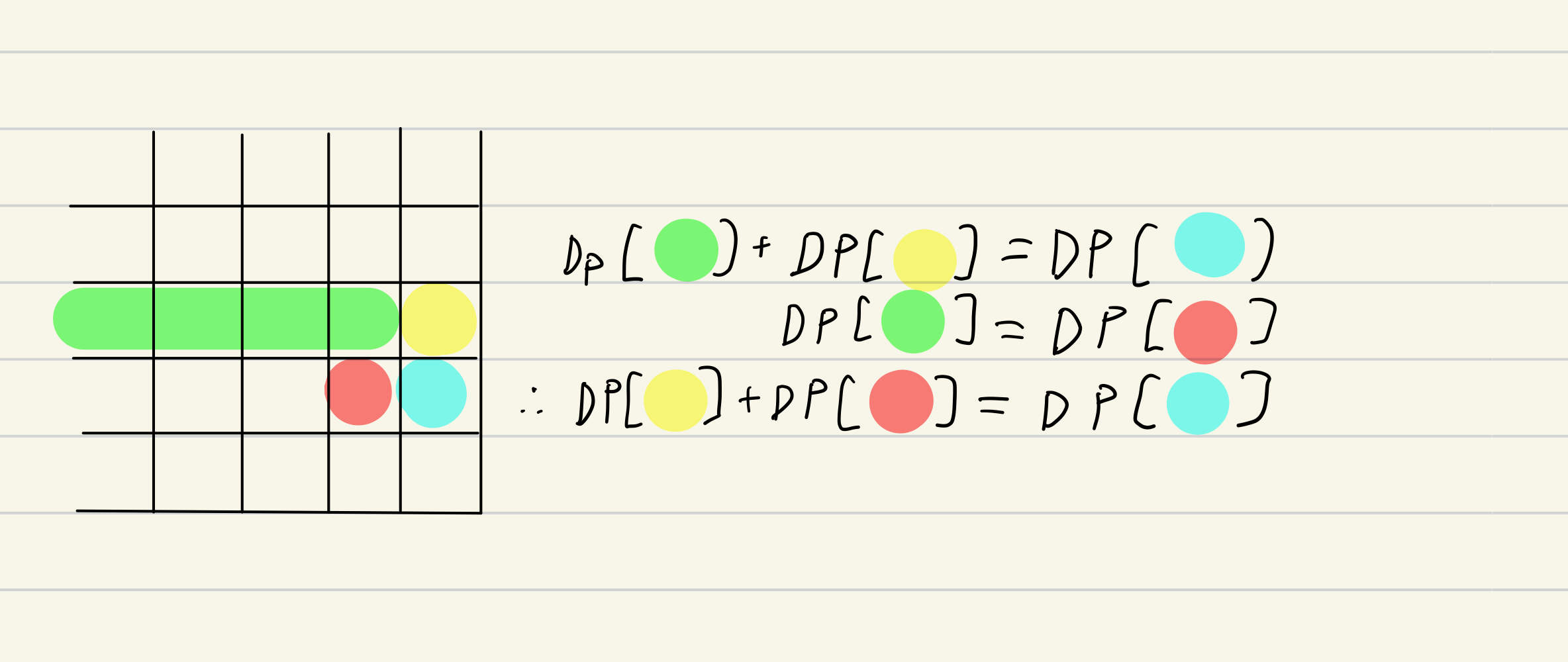
구간 DP


삽입 DP
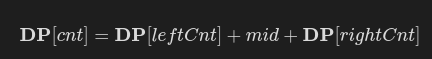

주의) DP의 점화식 형태가 이것들만 있다는 것이 아니라, 이러한 형태가 자주 나온다는 의미이니 주의하시길 바랍니다.
추천 문제
Easy
Normal
Hard
본 내용은 미국 정보 올림피아드인 USACO의 알고리즘 문제 학습 가이드인 usaco.guide를 참고하여 작성되었습니다.
'PS > USACO Gold' 카테고리의 다른 글
| [USACO Gold] DAG - 위상 정렬 (0) | 2025.10.07 |
|---|---|
| [USACO Gold] Disjoint Set, 분리 집합, Union-find (0) | 2025.10.07 |
| [USACO Gold] Knapsack DP - 배낭 문제를 다이나믹 프로그래밍으로 풀기 (0) | 2025.09.11 |
| [USACO Gold] 모듈러 연산, 모듈러 역원, 정수론에서의 합동 (0) | 2025.09.08 |
| [USACO Gold] Divisibility - PS(알고리즘)에서의 나눗셈 (0) | 2025.09.07 |