[USACO Gold] 모듈러 연산, 모듈러 역원, 정수론에서의 합동

모듈러 연산에서는 정수 그 자체로 계산하지 않고, 어떤 수를 m으로 나눈 나머지로 계산한다.

이를 "모듈러 m을 취한다”라고 부른다.

 

예를 들어 m=23이라면, x=247 대신 x  mod  23=17을 사용한다.
보통 m은 문제에서 주어지는 큰 소수(prime)이며, 가장 흔한 값은

• 1000000007
• 998 244 353=119⋅2^23+1

이다.
모듈러 산술은 내장 자료형의 범위를 넘는(오버플로) 큰 수를 다루지 않기 위해 사용되며, 다음 공식을 이용해 나머지를 취할 수 있다.

Modular Exponentiation (모듈러 거듭제곱)

거듭제곱 (Easy)

https://cses.fi/problemset/task/1095

CSES - Exponentiation

 

이진 거듭제곱(binary exponentiation)을 사용하면 거듭제곱 연산을 효율적으로 계산할 수 있다.
아이디어는 x^n을 이진수 구성요소로 분해하는 것이다.
예를 들어,

로 표현 가능하다.
그러면 y가 2의 거듭제곱인 모든 경우에 대해 x^y를 알고 있다면 O(log⁡n)에 x^n을 계산할 수 있다.

 

mmm을 함께 다루는 방법은, 모듈러가 곱셈에 대해 잘 동작한다는 점을 이용하면 된다.
위의 “이진 거듭제곱” 알고리즘을 그대로 구현하되, 중간 결과마다 (modm)을 취하는 한 줄만 추가하면 된다.

해설 - Exponentiation

import java.io.*;  

public class Exponentiation {  
    public static void main(String[] args) throws IOException {  
        int t;  
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));  
        PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));  

        t = Integer.parseInt(br.readLine());  

        StringBuilder sb = new StringBuilder();  
        while(t-->0){  
            sb.append(solve(br)).append('\n');  
        }  
        pw.println(sb);  
        br.close();  
        pw.close();  
    }  

    public static long solve(BufferedReader br) throws IOException {  
        String[] s = br.readLine().split(" ");  
        long a = Long.parseLong(s[0]);  
        long b = Long.parseLong(s[1]);  
        long m = 1000000007L;  

        long result = 1;  
        long now = a;  
        while(b > 0){  
            if((b & 1) == 1){  
                result *= now;  
                result %= m;  
            }  
            now = (now * now) % m;  
            b >>= 1;  
        }  
        return result;  
    }  
}

Modular Inverse (모듈러 역원)

모듈러 역원(modular inverse)은 실수에서의 역수(reciprocal)에 해당한다.
a를 b로 나누고 싶다면 a에 b의 모듈러 역원을 곱하면 된다.
여기서는 소수 모듈러스 p만 고려한다.

 

예를 들어 p=10^9+7에서 2의 역원은

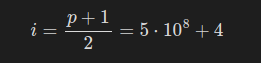
이다.

 

이는 임의의 정수 x에 대해

가 성립함을 뜻한다.
예시로 10i≡5(mod 10^9 + 7)이다.

직접 계산기로 찍어보면 와닿을 것이다.

거듭제곱을 이용한 모듈러 역원 구하는 방법

페르마의 소정리에 따르면, 소수 p로 나누어떨어지지 않는 모든 정수 a에 대해

가 성립한다.

페르마의 마지막 정리와 혼동하지 말자!

 

따라서, 다음 식으로 모듈러 역원을 구할 수 있다.

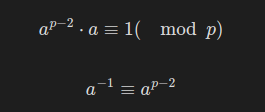
public class Main {
    public static final int MOD = (int)Math.pow(10, 9) + 7;
    public static void main(String[] args) throws IOException {
        long x = exp(2, MOD - 2, MOD);
        System.out.println(x);  // 500000004
        assert (2 * x % MOD == 1);
    }
}

유클리드 나눗셈을 이용한 방법

유클리드 나눗셈(확장 유클리드 알고리즘에서 유도)으로도 모듈러 역원을 구할 수 있다.
소수 모듈러스 m>a에 대해

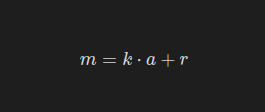
여기서

라고 하자. 그러면

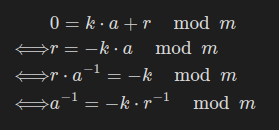
라고 할 수 있다.

위 식을 그대로 구현한 짧은 재귀 코드 예시는 다음과 같다

static int inv(int x) {
    return x <= 1 ? x : MOD - MOD/x * inv(MOD % x) % MOD;
}

이 접근의 장점은 구간 [1,MOD)의 역원을 O(MOD)에 미리 계산해둘 수 있다는 점이다.

inv[1] = 1;  // 이 배열은 이미 정의되어 있다고 가정
for (int i = 2; i < MOD; i++) { inv[i] = MOD - MOD / i * inv[MOD % i] % MOD; }

소수 p에 대한 모듈러 역원 계산은 보통 O(log⁡p) 시간이 걸리므로, 루프 안에서 빈번히 나눗셈을 수행하면 프로그램의 실행 시간이 크게 늘어날 수 있다.
동일한 수(들)의 역원을 여러 번 사용한다면 미리 계산해 두는 것이 좋다.

 

또한 0으로 나누지 않도록 항상 주의해야 한다. 모듈러를 취한 뒤에는 원래 0이 아니던 값이 0이 될 수도 있으므로, 상수가 아닌 값으로 나눌 때는 특히 조심해야 한다.

추천 문제

Easy

• https://cses.fi/problemset/task/1712
  • 해설: https://usaco.guide/problems/cses-1712-exponentiation-ii/solution

힌트
a^p = a mod p이다.
지수만 보면 b^c 가 p일 때 1이 된다.

Normal

• https://judge.yosupo.jp/problem/queue_operate_all_composite
  • 해설: https://usaco.guide/problems/ys-queue-composite/solution
• https://cses.fi/problemset/task/2182
  • 해설: https://usaco.guide/problems/cses-2182-divisor-analysis/solution

용어 정리

• 모듈러 연산
• 모듈러 역원
• 페르마의 소정리
• 유클리드 나눗셈

본 내용은 미국 정보 올림피아드인 USACO의 알고리즘 문제 학습 가이드인 usaco.guide를 참고하여 작성되었습니다.

Modular Arithmetic

궁금한 문제가 있으시거나 해설에 이해가 되지 않는 부분이 있다면 댓글 달아주시면 풀어드립니다.