MatMul 노드의 역전파는 그 결과를 보면 다소 비직관적이다.
따라서 이 MatMul의 역전파에 대해 좀 더 자세히 알아보자.
일단 MatMul 노드의 계산 그래프부터 확인해보자.

현재 우리에게 주어진 식은 아래와 같다.

- x = 1xD 행렬
- W = DxH 행렬
- y = 1xH 행렬
그리고, L에 대하여 x의 i번째 원소에 대한 편미분은 다음과 같이 구한다.

우리는 근데 y와 x 사이의 관계를 이미 알고있다.

따라서 위 식은 이렇게 치환이 가능하다.
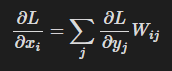
위 식에 의하여, L에 대하여 x의 i번째 원소에 대한 편미분의 경우 행렬곱을 이용해서 구해짐을 알 수 있게 된다.

그럼 이제 L에 대하여 가중치 W에 대한 편미분을 구할 차례이다.
이번엔 미니 배치 처리를 고려해 x에는 N개의 데이터가 담겨 있다고 가정해보자.
이를 계산 그래프로 표현하면 아래와 같다.

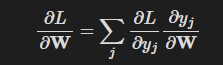
우리는 여기서도 y와 W사이의 관계를 이미 알고있다.

따라서 위 식은 이렇게 치환이 가능하다.

이쯤에서 형상을 어떤 식으로 맞춰야 할지 생각을 해보자.

위처럼 구성해야 형상을 잘 구성할 있음을 확인할 수 있었다.
이를 구현하면 아래와 같다.
class MatMul:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.x = None
def forward(self, x):
W, = self.params
out = np.matmul(x, W)
self.x = x
return out
def backward(self, dout):
W, = self.params
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
self.grads[0][...] = dW
return dx
'AI Repository > 기초 딥러닝' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝] seq2seq, Encoder-Decoder (0) | 2025.08.20 |
|---|---|
| [밑바닥부터 시작하는 딥러닝] LSTM (0) | 2025.08.17 |
| [밑바닥부터 시작하는 딥러닝] RNN (0) | 2025.08.15 |
| [밑바닥부터 시작하는 딥러닝] word2vec (0) | 2025.08.13 |
| [밑바닥부터 시작하는 딥러닝] 자연어와 단어의 분산 표현 (0) | 2025.08.12 |