본 내용은 밑바닥부터 시작하는 딥러닝 2도서를 참고하여 작성되었습니다.
밑바닥부터 시작하는 딥러닝 2 - 예스24
직접 구현하면서 배우는 본격 딥러닝 입문서 이번에는 순환 신경망과 자연어 처리다! 이 책은 『밑바닥부터 시작하는 딥러닝』에서 다루지 못했던 순환 신경망(RNN)을 자연어 처리와 시계열 데
www.yes24.com
망각은 더 나은 전진을 낫는다.
- 니체 -
RNN의 문제점
RNN은 시계열 데이터의 장기 의존 관계를 학습하기 어렵다.
BPTT에서 기울기 소실 혹은 기울기 폭발이 일어나기 때문이다.
이번 절에서는 앞장에서 배운 RNN을 복습하고, RNN이 장기기억을 처리하지 못하는 이유를 알아보자.
RNN 복습
RNN계층은 순환 경로를 갖고 있다.
그리고 그 순환을 펼치면 다음과 같이 옆으로 길게 뻗은 신경망이 만들어진다.

RNN계층은 시계열 데이터인 x_t를 입력하면 h_t를 출력한다.
이 h는 동시에 계층 내에 저장되기도 하는데, 그래서 이 h를 은닉 상태라고 하며, 현재 입력받은 과거 정보(맥락)을 저장한다.
RNN은 이 은닉상태를 이용한다.
이를 계산 그래프로 나타내면 아래와 같다.

기울기 소실 또는 기울기 폭발
앞장에선 RNNLM을 구현했다.
이번 절에선 RNNLM의 단점을 확인하는 차원에서 이 문제를 다시 봐보자.

앞에서도 나왔듯이 빈칸에 들어갈 단어는 "Tom"이다.
근데 RNNLM이 이 문제를 풀려면, 다음 맥락을 알아야 한다.
- Tom이 방에서 TV를 보고 있었음
- 마리가 방에 들어옴
다시말해, 이 정보를 RNN 계층의 은닉 상태에 보관해두어야 한다.
이 문제를 "RNNLM 학습"의 관점에서 생각해보자.
여기에서는 정답 레이블로 "Tom"이라는 단어가 주어졌을 때, RNNLM에서 기울기가 어떻게 전파되는지 살펴보자.
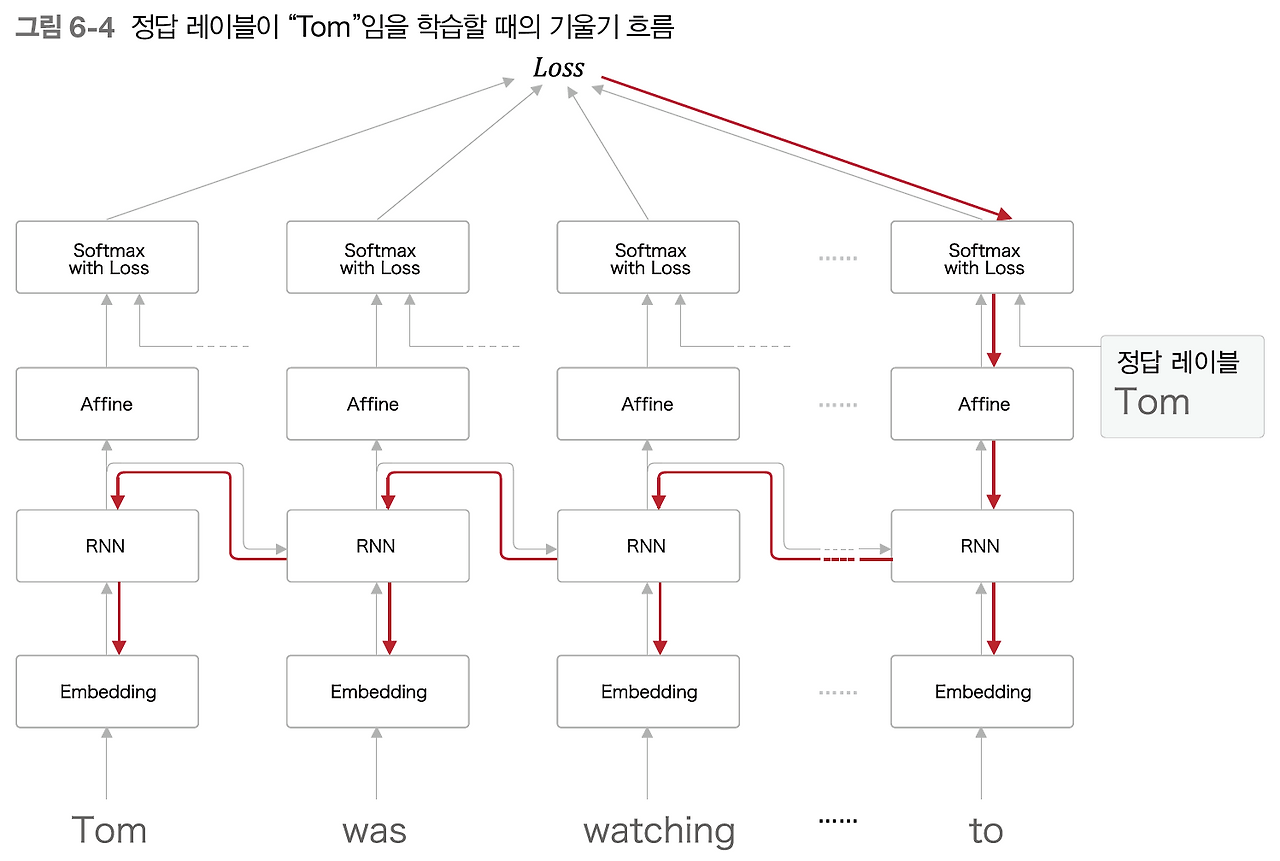
Tom이라는 정보를 가지고 있기 위해서, 수많은 문맥을 거쳐야 했다.
하지만 만약 기울기가 중간에 0에 가까워지면, 가중치 매개변수는 전혀 갱신되지 않게 된다.
즉, 장기 의존 관계를 학습할 수 없게 된다.
기울기 소실과 기울기 폭발의 원인
좀 더 논리적으로 RNN 계층에서 기울기 소실/폭발이 일어나는 원인을 살펴보자.
아래 그림과 같이 RNN계층에서의 시간 방향 기울기 전파에만 주목해보자.

길이가 T인 시계열 데이터를 가정하여 T번째 정답 레이블로부터 전해지는 기울기가 어떻게 변화하는지 보자.
- tanh
- +
- 행렬곱(MatMul)
이 연산을 차례대로 통과한다.
잠깐 하이퍼볼릭 탄젠트의 그래프를 살펴보면 아래와 같다.
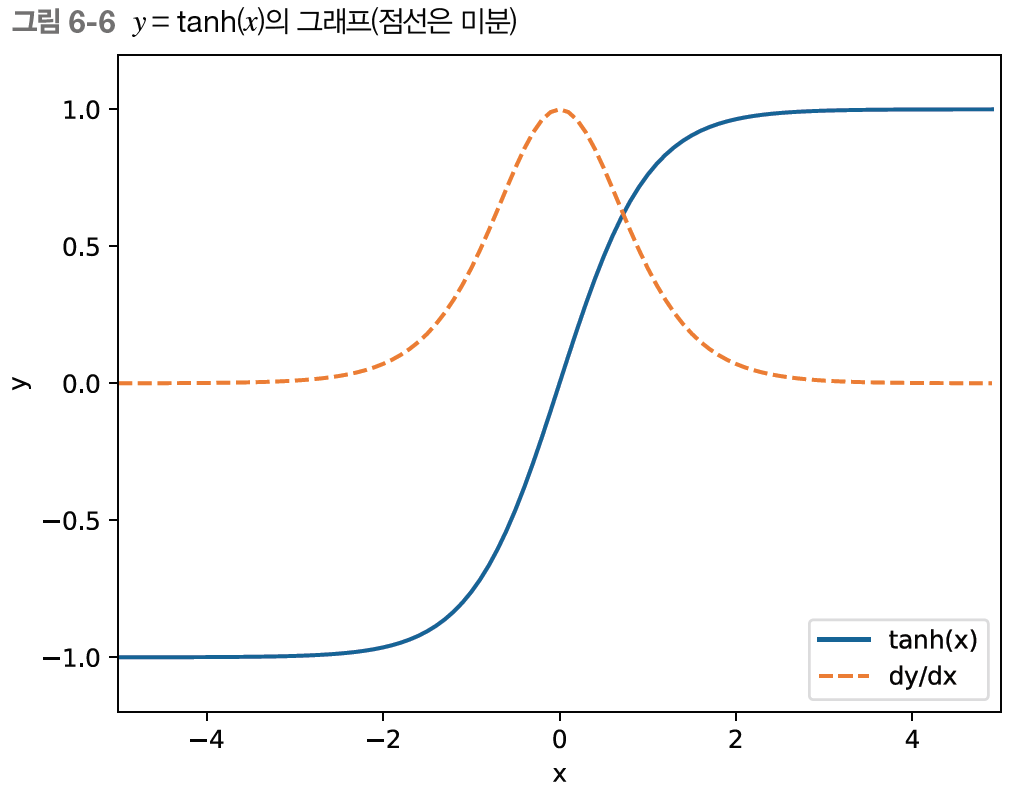
보다시피 그 값은 1.0 이하이고, x가 0으로부터 멀어질수록 작아진다.
달리 말하면, 역전파에서는 기울기가 tanh 노드를 지날 때마다 값은 계속 작아진다는 것이다.
그래서 tanh 함수를 T번 통과하면 기울기도 T번 반복해서 작아지게 된다.
RNN계층의 활성화 함수로는 주로 tanh 함수를 사용하는데, 이를 ReLU로 바꾸면 기울기 소실을 줄일 수 있다. 실제로 "Improving performance of recurrent neural network with relu nonlinearity" 논문에서는 ReLU를 이용해 성능을 개선했다.
다음은 MatMul 차례이다. 여기에서는 이야기를 단순화하기 위해 tanh를 무시하도록 하자.

상류로부터 dh라는 기울기가 흘러온다고 가정하자.
이때 MatMul노드에서의 역전파는 dhW_h^T 라는 행렬곱으로 기울기를 계산한다.
그리고 같은 계산을 시계열 데이터의 크기만큼 반복한다.
여기에서 주목할 점은 이 행렬 곱셈에서는 매번 똑같은 가중치인 W_h가 사용된다는 것이다.
그럼 역전파 시 기울기는 MatMul 노드를 지날 때마다 어떻게 변화할까?
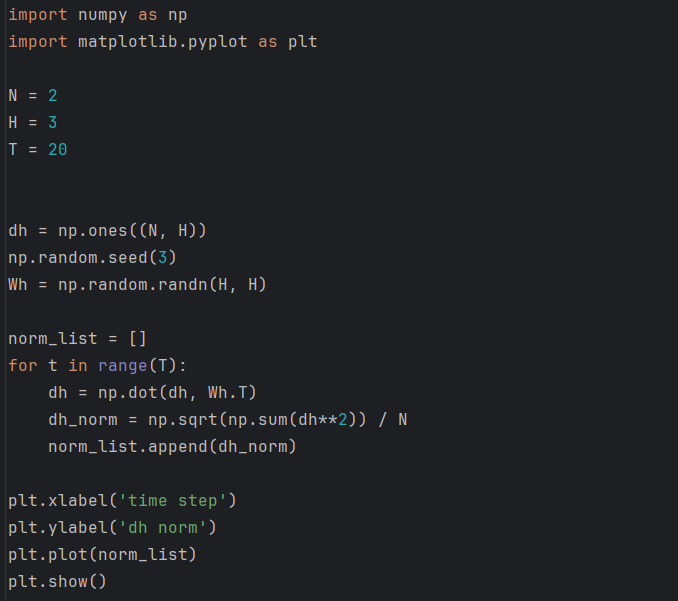

위 그림에서 보듯 기울기의 크기가 시간에 비례해 지수적으로 증가한다.
이것이 바로 기울기 폭발(exploding gradients)이다.
이러한 기울기 폭발이 일어나면 결국 오버플로우를 일으켜 NaN같은 값을 발생시킨다.
이번엔 Wh의 초깃값을 살짝 바꿔서 진행해보자.
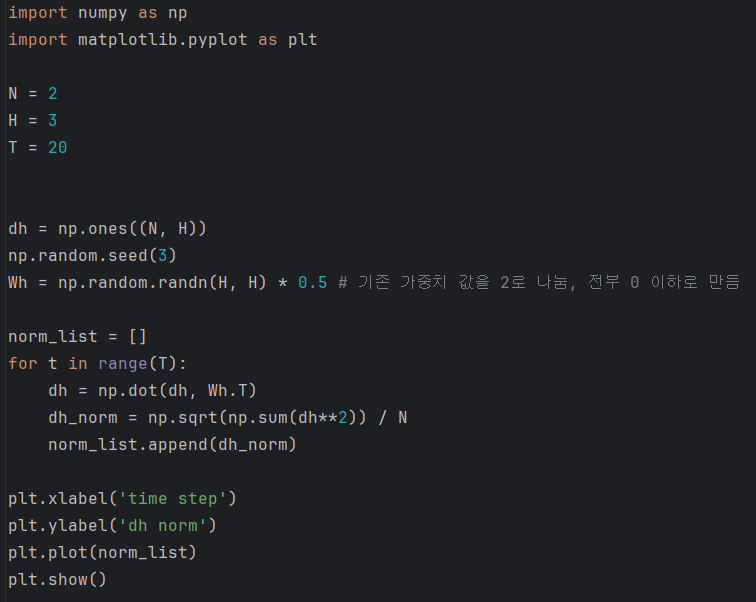
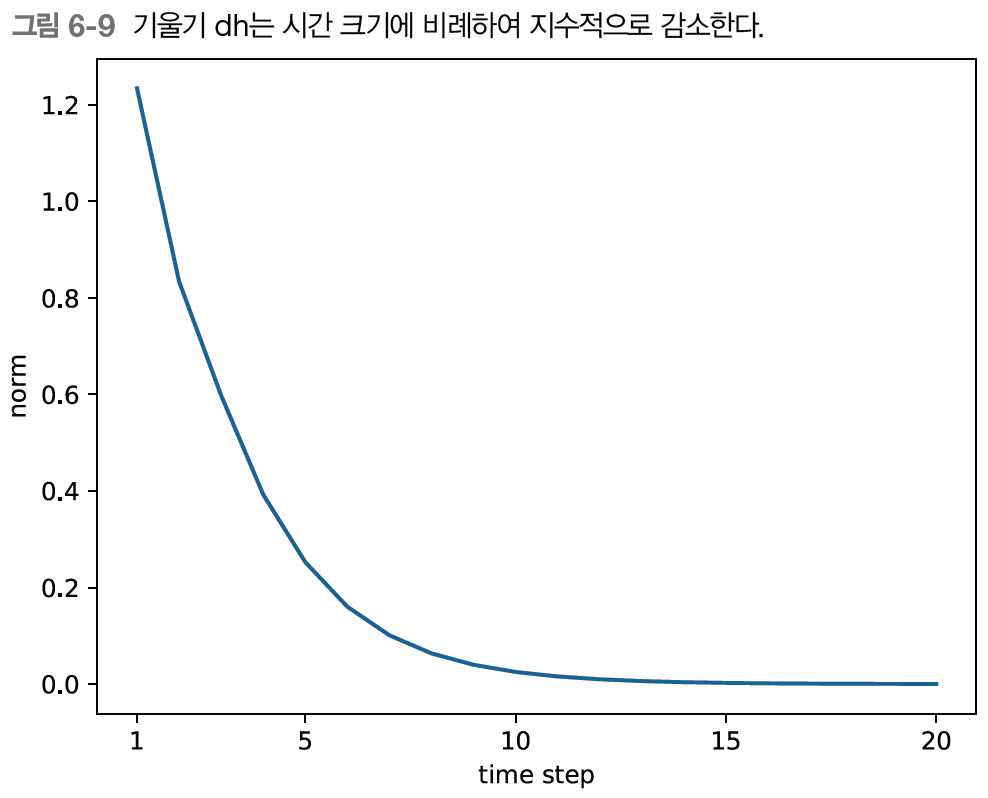
이번에는 기울기가 지수적으로 감소한다.
이것이 기울기 소실(vanishing gradients)이다.
왜 이런 지수적인 변화가 발생했을까?
물론 Wh를 T번 반복해서 '곱'했기 때문이다.
만약 Wh가 스칼라라면 이야기는 단순해지는데, Wh가 1보다 크면 지수적으로 증가하고, 1보다 작으면 지수적으로 감소한다.
그럼 Wh가 스칼라가 아니라 행렬이라면 어떨까?
이 경우, 행렬의 '특잇값'이 척도가 된다.
행렬의 특잇값이란, 간단히 말하면 데이터가 얼마나 퍼져 있는지를 나타낸다.
이 특잇값의 값 중 최댓값이 1보다 큰지 여부를 보면 크기가 어떻게 변할지 예측할 수 있다.
우리가 과거 word2vec 학습 시 통계적 근사치를 구했던 특잇값 분해에서, 가운데 대각행렬이 특잇값들이다.
참고로 특잇값이 1보다 크다고 반드시 기울기가 폭발하고, 1보다 작다고 반드시 기울기가 소실하는 것은 아니다.
즉, 필요조건일 뿐 충분조건은 아니다.
기울기 폭발 대책
지금까지 기울기 폭발과 기울기 소실에 대해서 알아보았다.
그럼 계속해서, 그 해결책을 알아보겠다.
기울기 폭발은 소실에 비해 비교적 해결책이 간단한데, 의사코드로 표현하면 아래와 같다.

여기에서는 신경망에서 사용되는 모든 매개변수에 대한 기울기를 하나로 처리한다고 가정하고, 이를 기호 g hat으로 표시했다.
그리고 threshold를 문턱값으로 설정했다.
이때 기울기의 L2 노름이 문턱값을 초과하면 두번째 줄의 수식과 같이 기울기를 수정한다.
보다시피 단순한 알고리즘이지만, 많은 경우에 잘 작동한다.
그럼 이제 기울기 클리핑을 파이썬으로 구현해보자.

이상으로 기울기 폭발과 그 해결책인 기울기 클리핑에 대한 설명을 마치겠다.
기울기 소실과 LSTM
RNN 학습에서는 기울기 소실도 큰 문제이다. 그리고 이 문제를 해결하려면 RNN계층의 아키텍처를 근본부터 뜯어고쳐야 한다.
여기서 등장하는 것이, 이번 장의 핵심 주제인 '게이트가 추가된 RNN'이다.
게이트가 추가된 RNN으로는 많은 아키텍처가 있으며, 대표적으로 다음 두가지가 있다.
- LSTM
- GRU
이번 장에서는 LSTM에 집중하면서, LSTM이 기울기 소실을 일으키지 않는(일으키기 어렵게 하는) 원리를 살펴보자.
계산 그래프 단순화
시작하기 전에, 모든 연산을 전부 계산 그래프로 그리면 가독성이 떨어진다.
이번 절에서는 행렬 계산이나 알려진 함수를 아래와 같이 단순화된 직사각형 노드로 정리해 그리도록 하겠다.

위 그림은 선형 함수 + tanh 연산을 [tanh] 라는 직사각형 노드 하나로 그렸다.
LSTM 인터페이스
이제 LSTM의 인터페이스(입출력)에 대해 알아보자.

위 그림에서 보듯, LSTM 계층에 인터페이스에는 c라는 경로가 추가로 존재한다.
이 c를 기억 셀(memory cell)이라 하며, LSTM 전용의 기억 메커니즘이다.
기억 셀의 특징은 데이터를 자기 자신으로만(LSTM 계층 내에서만) 주고받는다는 것이다.
즉, LSTM 계층 내에서만 완결되고, 다른 계층으로는 출력하지 않는다.
반면, LSTM의 은닉상태 h는 RNN계층과 마찬가지로 다른 계층으로(위쪽으로) 출력된다.
LSTM의 출력을 받는 쪽에서 보면 LSTM의 출력은 은닉 상태 벡터 h 뿐이다.
기억 셀 c는 외부에서는 보이지 않는다. 그래서 외부는 그 존재 자체를 생각할 필요가 없다.
LSTM 계층 조립하기
LSTM의 인터페이스를 살펴보았으니, 이제 LSTM의 내부 구성요소들을 하나씩 살펴보며 LSTM을 이해해보자.
LSTM은 기억 셀 c_t가 있다. 이 c_t에는 시각 t에서의 LSTM의 기억이 저장돼 있는데, 과거로부터 시각 t까지에 필요한 모든 정보가 저장돼 있다고 가정한다(혹은 그렇게 되도록 학습을 수행한다).
그리고 필요한 정보를 모두 간직한 이 기억을 바탕으로, 외부 계층에(그리고 다음 시각의 LSTM에) 은닉상태 h_t를 출력한다. 이때 출력하는 h_t는 아래 그림과 같이 기억 셀의 값을 tanh 함수로 변환한 값이다.
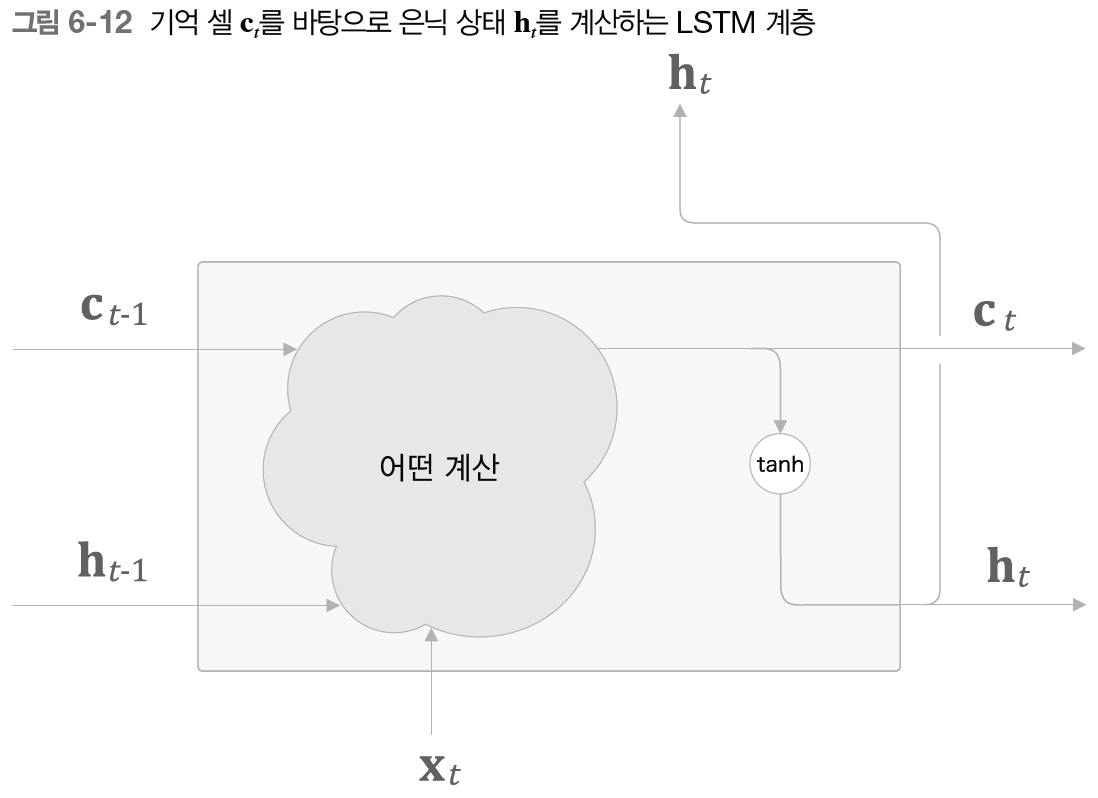
위 그림처럼 현재의 기억 셀 c_t에는 3개의 입력(c, h, t)으로부터 '어떤 계산'을 수행하여 구할 수 있다.
여기서 핵심은 갱신된 c_t를 사용해 은닉상태 h_t를 계산한다는 것이다.
또한 이 계산은 아래와 같다.
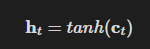
이는 c_t의 각 요소에 tanh를 적용한다는 뜻이다.
이 말은, 기억셀 c_t와 은닉 상태 h_t의 원소 수가 같다는 것이다.
예를들어 기억 셀 c_t의 원소가 100개면 은닉상태 h_t의 원소 수도 100개가 된다.
게이트
진도를 더 나가기 전에, '게이트'라는 개념에 대해 간단하게 알아보자.
게이트는 데이터의 흐름을 제어한다.
마치 아래 그림처럼 물의 흐름을 멈추거나 배출하는 역할을 수행한다.

LSTM에서 게이트는 '열기/닫기' 뿐 아니라, 어느 정도 열지를 조절할 수 있다.
이 '어느 정도'를 '열림 상태'(openness)라 부르며, 아래 그림처럼 비율을 제어할 수 있다.

중요한 점은, 이 얼마나 열리는가 (0.0~1.0)도 내부 파라미터로, 이 전용 가중치 매개변수는 학습 데이터로부터 갱신된다.
참고로 게이트의 열림 상태를 구할 때는 시그모이드 함수를 사용하는데, 시그모이드 함수의 출력이 마침 0.0~1.0 사이의 실수이기 때문이다.
LSTM에는 다음 3가지 종류의 게이트가 들어간다.
- output 게이트
- forget 게이트
- input 게이트
LSTM을 하나씩 조립해가며, 다양한 게이트들을 만나보자.
output 게이트
바로 앞에서 은닉 상태 h_t는 기억셀 c_t에 단순히 tanh 함수를 적용했을 뿐이라고 설명했다.
그럼 이제 이 은닉 상태에 게이트를 적용해보자.
즉, tanh(c_t)의 각 원소에 대해 '그것이 다음 시각의 은닉 상태에 얼마나 중요한가'를 조정해보자.
한편, 이 게이트는 다음 은닉 상태 h_t의 출력을 담당하는 게이트이므로 output 게이트라고 한다.
output 게이트의 열림 상태(openness)는 입력 x_t와 이전 상태 h_t-1 로부터 구한다.
이때의 계산은 아래 식과 같다.

참고로, 위첨자로 o가 들어간 가중치와 편향은 위에서 설명한 대로 게이트를 위한 전용 가중치와 편향이다.
이상을 계산 그래프로 그리면 아래와 같을 것이다.

위 시그마가 아웃풋 게이트 연산을 수행한다.
즉, 아래와 같은 과정으로 이루어진다.
- "어떠한 계산"(ex: 가중치와 편향을 이용한 선형 변환)을 수행한다.
- 아웃풋 게이트를 통과하며, 그 값을 반영할 범위를 결정한다.
이때, 아웃풋 게이트 통과는 "아다마르 곱"을 통해 이루어지며, 수식으로는 아래와 같다.

아다마르 곱은 "행렬의 원소별 곱셈"으로 이해하면 쉽다.
이상이 LSTM의 output 게이트이다.
이제 LSTM의 출력 부분은 완성되었다.
이제 기억 셀 갱신 부분을 살펴보자.
tanh 함수는 (-1, 1) 범위를 갖는다.
그래서 정보의 "강약" 을 조절하는데 이용한다.
sigmoid는 (0, 1) 범위를 갖는다.
그래서 정보의 "비중"을 조정하는데 이용한다.
forget 게이트
망각은 더 나은 전진을 낳는다. 우리가 다음에 해야 할 일은 기억 셀에 '무엇을 잊을까'를 명확하게 지시하는 것이다.
이런 일도 물론 게이트를 사용해 해결한다.
그럼 c_t-1 의 기억 중에서 불필요한 기억을 잊게 해주는 게이트를 정의한다.
이를 forget 게이트라고 한다.
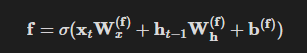
이를 계산 그래프로 표현하면 아래와 같다.

이 게이트를 통과하면 게이트의 출력 f가 구해진다.
그리고 이 f와 이전 기억 셀인 c_t-1 과의 아다마르 곱을 통해 c_t를 구한다.
새로운 기억 셀
forget 게이트를 거치면서 이전 시각의 기억 셀로부터 잊어야 할 기억이 삭제되었다.
그런데 이 상태로는 기억 셀이 잊는 것밖에 하지 못하기 때문에(새로운 기억을 추가해야 한다!), 이번에 계산할 뉴런 노드를 추가하여 f와 더해주어야 한다.
그래서 tanh 박스 노드를 추가했고, 이를 기존 기억에 더했다.
계산 그래프로 표현하면 아래와 같다.
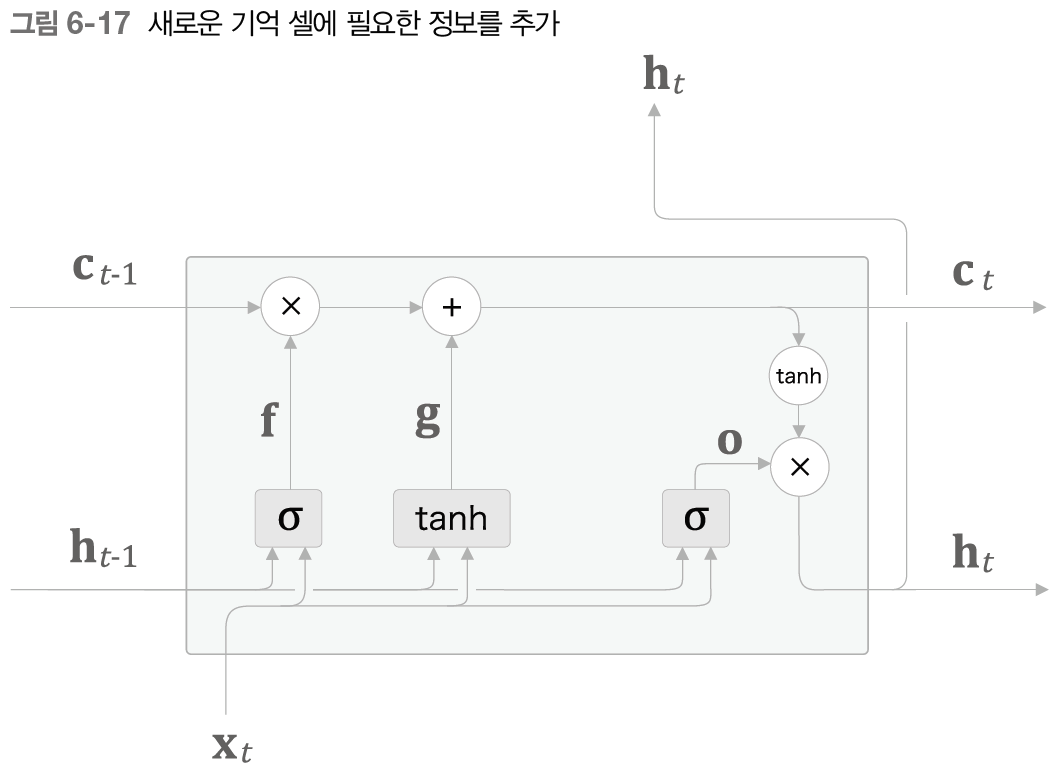
여기서 추가된 tanh 노드는 "게이트"가 아니다.
새로운 '정보'를 기억 셀에 추가하는 것이 목적이기 때문에, 활성화 함수로는 시그모이드 함수가 아닌 tanh 함수를 사용한다.
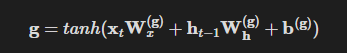
이 새로운 기억 g가 이전 시각의 기억 셀인 c_t-1에 더해짐으로써 새로운 기억이 생겨난다.
input 게이트
마지막으로 g에 게이트를 하나 추가할 생각이다.
input 게이트를 추가하면 계산 그래프가 아래처럼 변한다.

즉, g를 그대로 바로 쓰지 않고, 이것도 비중을 조정해서 추가한다.
input게이트는 g의 각 원소가 새로 추가되는 정보로써의 가치가 얼마나 큰지를 판단한다.
새 정보를 무비판적으로 수용하는 게 아니라, 적절히 취사선택하는 것이 이 게이트 역할의 핵심이다.
이를 수식으로 나타내면 아래와 같다.

이상이 LSTM의 연산 처리 과정이다.
LSTM의 기울기 흐름
지금까지 LSTM의 구조를 살펴봤는데, 이게 어떻게 기울기 소실을 없애주는(완화해주는) 걸까?
그 원리는 기억 셀 c의 역전파에 주목하면 보인다.
위 그림에서 기억 셀의 역전파를 자세히 보면, 비선형 함수를 지나지 않는다.
덧셈 노드는 상류에서 전해지는 기울기를 그대로 흘릴 뿐이기에, 기울기 변화(감소)는 일어나지 않는다.
곱셈 노드는 행렬 곱이 아닌 아다마르 곱을 계산하기에, 곱셈의 효과가 누적되지 않아 0에 가까운 기울기의 영향이 지나치게 커지지 않게 막는다.
게다가 곱셈 노드의 계산은 forget 게이트가 제어한다.(그리고 매 시각 다른 게이트 값을 출력한다.)
그리고 forget 게이트가 '잊어야 한다'고 판단한 기억 셀의 원소에 대해서는 그 기울기가 작아지는 것이다.
한편, forget 게이트가 '잊어서는 안된다'고 판단한 원소에 대해서는 그 기울기가 약회되지 않은 채로 과거 방향으로 전해진다.
따라서 기억 셀의 기울기가 (오래 기억해야 할 정보일 경우) 소실 없이 전파되리라 기대할 수 있다.
LSTM은 Long Short-Term Memory의 줄임말이다.
이 용어는 단기 기억을 긴 시간동안 지속할 수 있음을 의미한다.
LSTM 구현
그럼 LSTM을 구현해보자.

그 전에 위 네 식에서 공통적으로 포함된 수식을 보자.

이를 "아핀 변환"(Affine transformation)이라고 하는데, 행렬 변환과 평행 이동을 결합한 형태의 식을 의미한다.
이 아핀 변환을 하나의 식으로 정리할 수 있다.
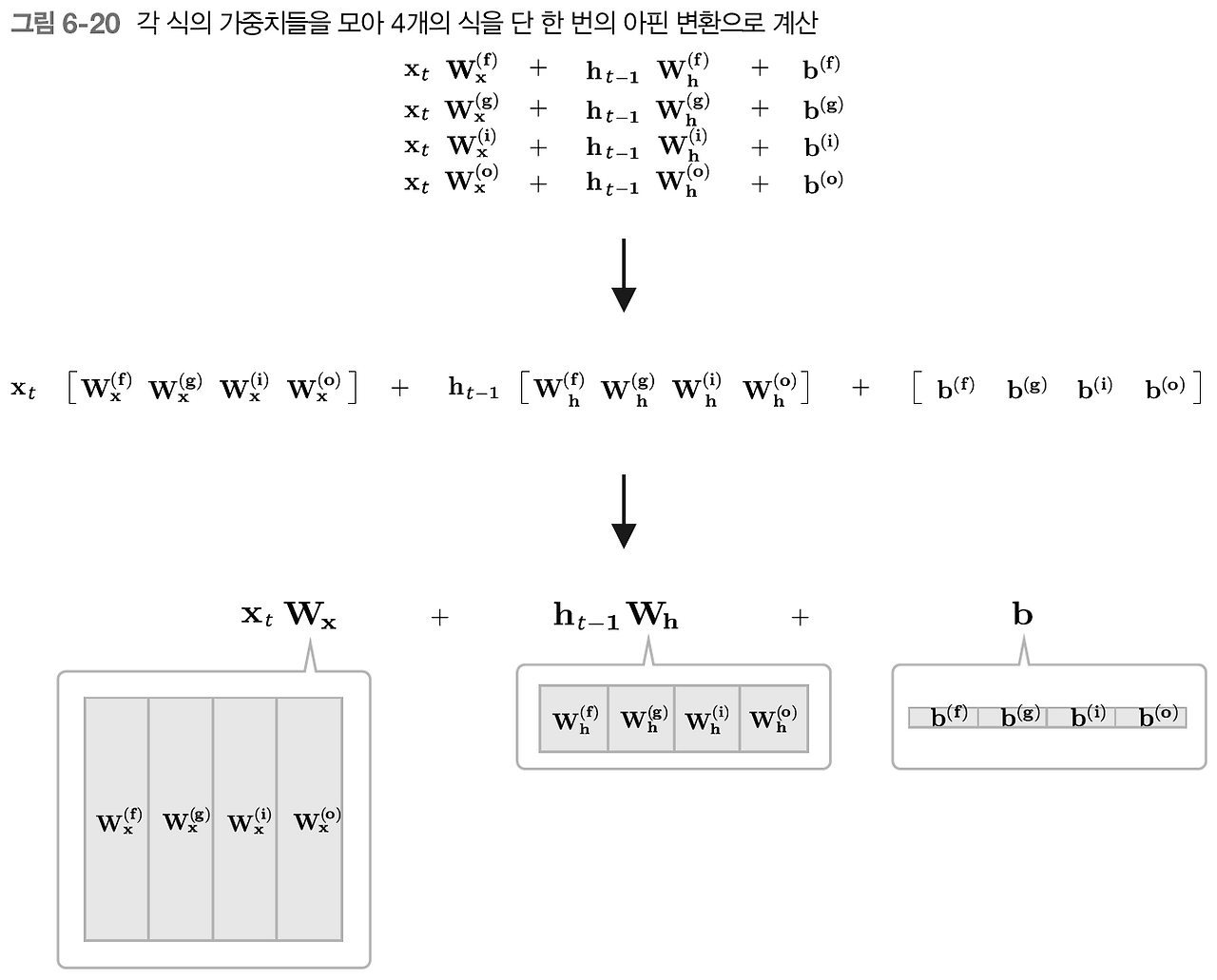
이를 그림으로 표현한 것이 아래 그림이다.

이렇게 하면 원래 개별적으로 총 4번을 수행하던 아핀 변환을 단 1회의 계산으로 끝마칠 수 있다.
계산 속도가 빨라진다는 뜻이다.
왜냐하면 일반적으로 행렬 라이브러리는 '큰 행렬'을 한꺼번에 계산할 때가 각각을 따로 계산할 때보다 빠르기 때문이다.
한편, 가중치를 한 데로 모아 관리하게 되어 소스 코드도 간결해진다.
그럼 W_x, W_h, b 각각에 4개분의 가중치(혹은 편향)가 포함되어 있다고 가정하고, 이때의 LSTM을 계산 그래프로 그려보면 아래처럼 된다.

위 그림에서 보듯, 처음에는 4개분의 아핀 변환을 한꺼번에 수행한다.
그리고 slice 노드를 통해 그 4개의 결과를 꺼낸다.
slice 노드 다음에는 활성화 함수를 거쳐 앞 절에서 설명한 계산을 수행한다.
그럼 위 그림을 참고하여 초기화 메소드부터 구현하자.
모든 가중치를 한 행렬 안에 받을 것이다.

기존에 구현하였던 것들과 형태가 유사해졌다.
이어서 순전파 구현을 수행해보자.
순전파는 현 시각의 입력 x, 이전 시각의 은닉 상태 h_prev, 이전 시각의 기억 셀 c_prev를 받는다.

이 메소드에선
- 먼저 아핀 변환을 수행하고,
- 활성화 함수를 적용한 뒤,
- 이를 slice하여 역전파용 캐시에 저장한다.
이후 다음 은닉 상태와 기억 셀을 반환한다.
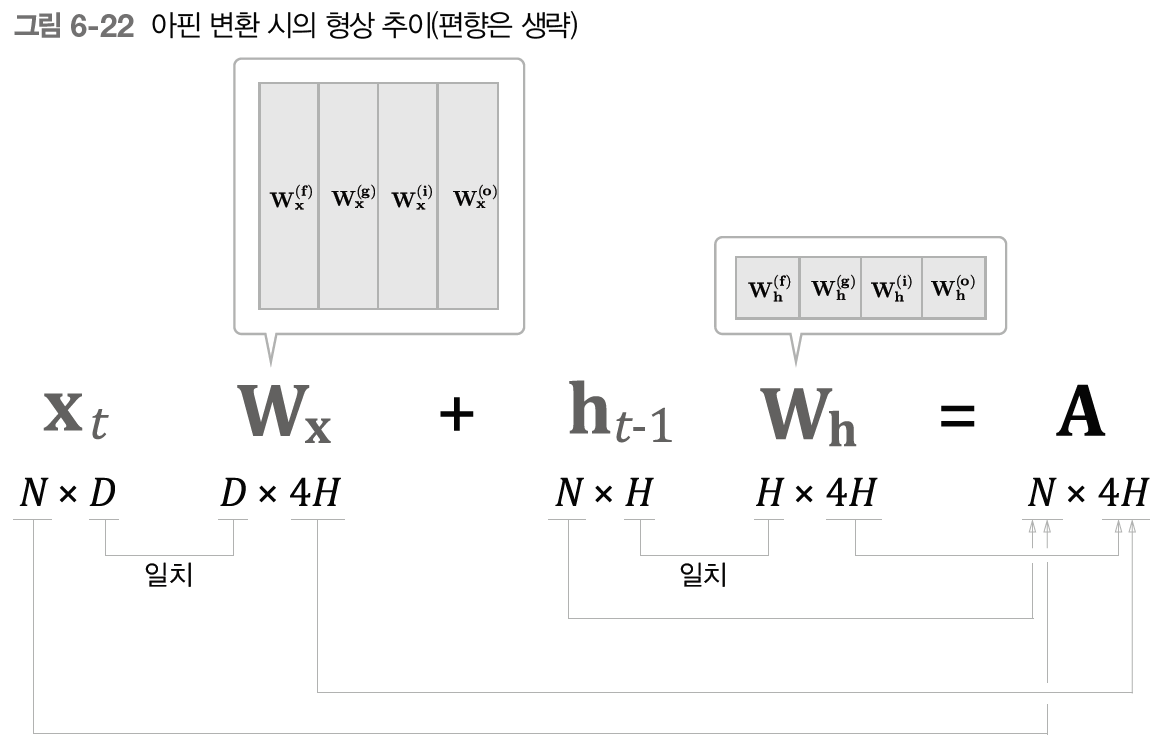
위에서 우리는 slice를 이용해 행렬을 네 조각으로 나눠서 분배했다.
따라서 그 역전파에서는 반대로 4개의 기울기를 결합해야 한다.

이를 numpy로 수행하려면, np.hstack() 메소드를 사용하면 된다.
np.hstack()은 인수로 주어진 배열을 가로로 연결한다.
따라서 이 처리를 다음의 한 줄로 끝낼 수 있다.
dA = np.hstack((df, dg, di, do))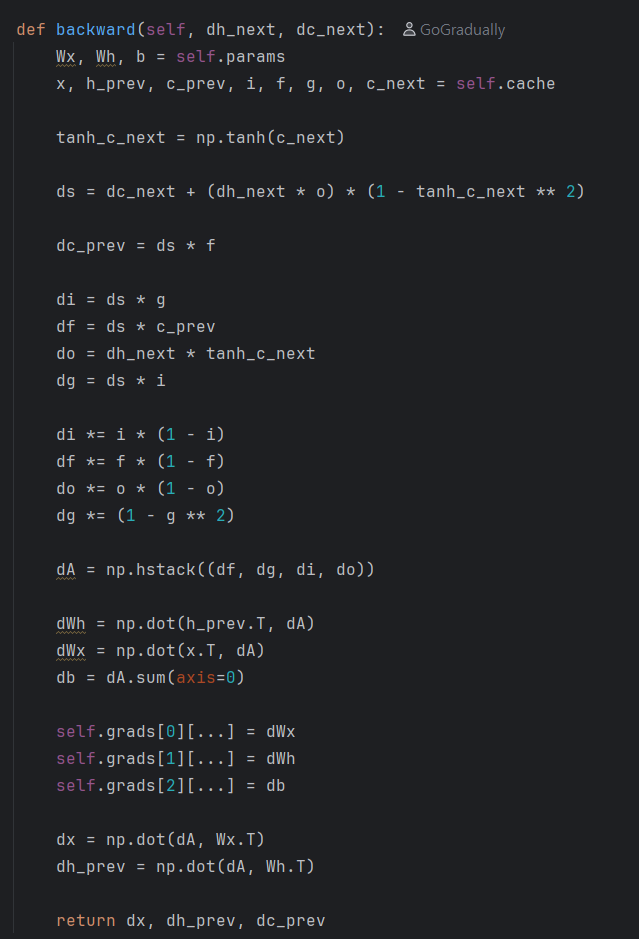
Time LSTM 구현
Time LSTM은 T개분의 시계열 데이터를 한꺼번에 처리하는 계층이다.
전체 그림은 아래와 같다.

이번에도 Truncated BPTT를 사용할 것이기에, 은닉 상태와 기억 셀을 인스턴스 변수로 유지하도록 하겠다.

class TimeLSTM:
def __init__(self, Wx, Wh, b, stateful=False):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.c = None, None
self.dh = None
self.stateful = stateful
def forward(self, xs):
Wx, Wh, b = self.params
N, T, D = xs.shape
H = Wh.shape[0]
self.layers = []
hs = np.empty((N, T, H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
if not self.stateful or self.c is None:
self.c = np.zeros((N, H), dtype='f')
for t in range(T):
layer = LSTM(*self.params)
self.h, self.c = layer.forward(xs[:, t, :], self.h, self.c)
hs[:, t, :] = self.h
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D = Wx.shape[0]
dxs = np.empty((N, T, D), dtype='f')
dh, dc = 0, 0
grads = [0, 0, 0]
for t in reversed(range(T)):
layer = self.layers[t]
dx, dh, dc = layer.backward(dhs[:, t, :] + dh, dc)
dxs[:, t, :] = dx
for i, grad in enumerate(layer.grads):
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs
def set_state(self, h, c=None):
self.h, self.c = h, c
def reset_state(self):
self.h, self.c = None, None이제 이 TimeLSTM을 이용한 언어 모델을 만들어보자.
LSTM을 사용한 언어 모델
먼저, 기존 RNN과 LSTM을 비교해보자.
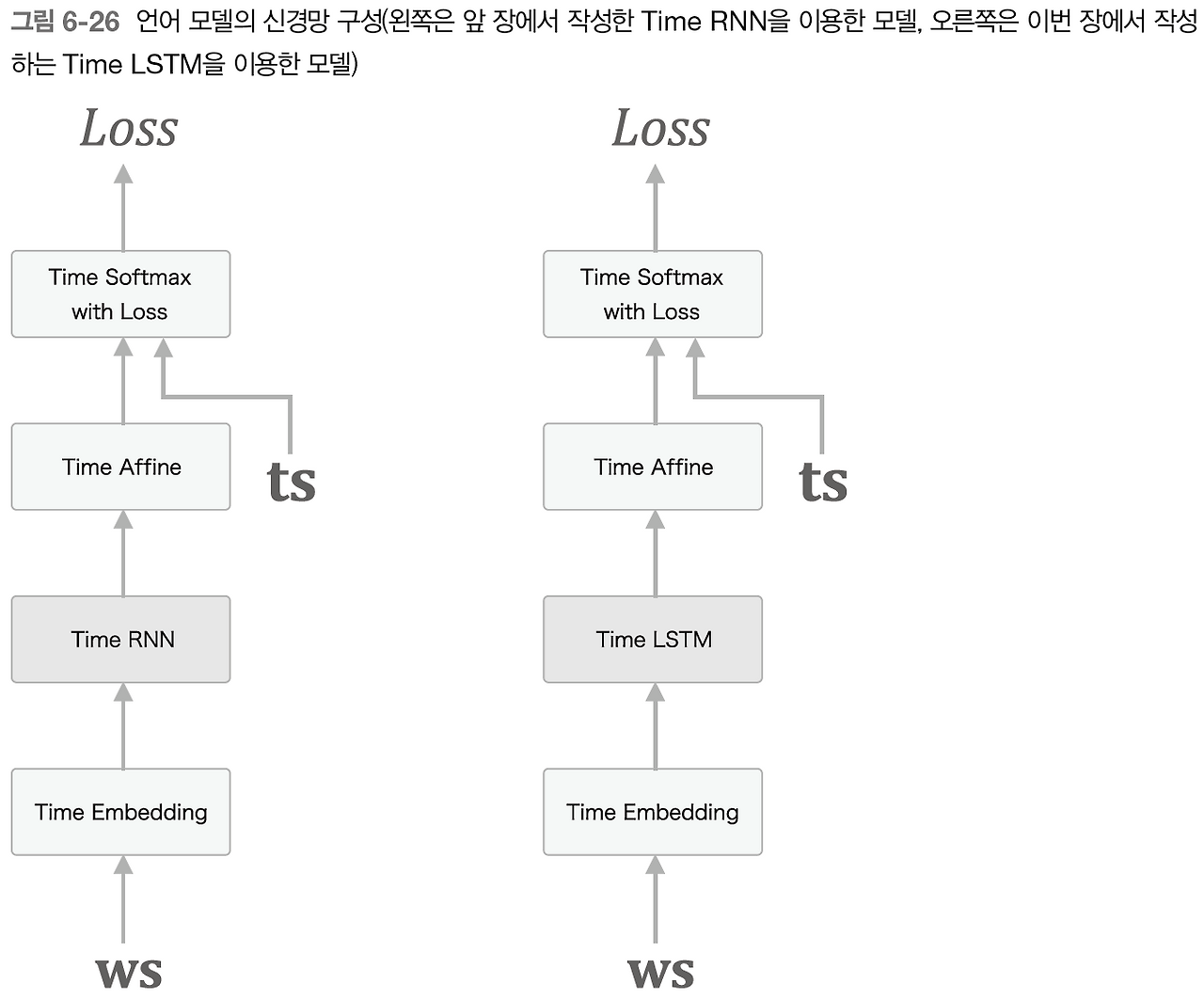
위 그림에서 보듯이, 전체 구현에서 차이는 TimeRNN->TimeLSTM으로 바뀐 것 외에는 차이가 없다.
LSTM 계층을 사용하는 Rnnlm 클래스의 구현을 보자.
import sys
sys.path.append('..')
from common.time_layers import *
import pickle
class Rnnlm:
def __init__(self, vocab_size=10000, wordvec_size=100, hidden_size=100):
V, D, H = vocab_size, wordvec_size, hidden_size
rn = np.random.randn
embed_W = (rn(V, D)/ 100).astype('f')
lstm_Wx = (rn(D, 4*H)/ np.sqrt(D)).astype('f')
lstm_Wh = (rn(H, 4*H)/ np.sqrt(H)).astype('f')
lstm_b = np.zeros(4*H).astype('f')
affine_W = (rn(H, V)/ np.sqrt(H)).astype('f')
affine_b = np.zeros(V).astype('f')
self.layers = [
TimeEmbedding(embed_W),
TimeLSTM(lstm_Wx, lstm_Wh, lstm_b, stateful=True),
TimeAffine(affine_W, affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss()
self.lstm_layer = self.layers[1]
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self, xs):
for layer in self.layers:
xs = layer.forward(xs)
return xs
def forward(self, xs, ts):
score = self.predict(xs)
loss = self.loss_layer.forward(score, ts)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
def reset_state(self):
self.lstm_layer.reset_state()
def save_params(self, file_name="Rnnlm.pkl"):
with open(file_name, 'wb') as f:
pickle.dump(self.params, f)
def load_params(self, file_name="Rnnlm.pkl"):
with open(file_name, 'rb') as f:
self.params = pickle.load(f)Rnnlm 클래스에는 softmax 계층 직전까지를 처리하는 predict() 메소드가 추가되었다.
이 메소드는 7장에서 수행하는 문장 생성에 사용된다.
그리고 매개변수 읽기/쓰기를 처리하는 load_params()와 save_params()메소드도 추가되었다.
나머지는 앞장의 SimpleRNNLM 클래스와 같다.
이제 이 신경망을 사용해 PTB데이터셋을 학습시켜보자.
이번엔 PTB 데이터셋의 전부를 사용한다!
학습을 위한 코드는 아래와 같다.
import sys
sys.path.append('..')
from common import config
config.GPU = True
from common.optimizer import SGD
from common.trainer import RnnlmTrainer
from common.util import eval_perplexity
from dataset import ptb
from rnnlm import Rnnlm
# 하이퍼파라미터 설정
batch_size = 20
wordvec_size = 100
hidden_size = 100
time_size = 35
lr = 20
max_epoch = 4
max_grad = 0.25
# 학습 데이터 읽기
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_test, _, _ = ptb.load_data('test')
vocab_size = len(word_to_id)
xs = corpus[:-1]
ts = corpus[1:]
# 모델 생성
model = Rnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)
# 기울기 클리핑 적용하여 학습
trainer.fit(xs, ts, max_epoch, batch_size, time_size, max_grad, eval_interval=20)
trainer.plot(ylim=(0, 500))
# 테스트 데이터로 평가
model.reset_state()
ppl_test = eval_perplexity(model, corpus_test)
print('테스트 퍼플렉서티: ', ppl_test)
# 매개변수 저장
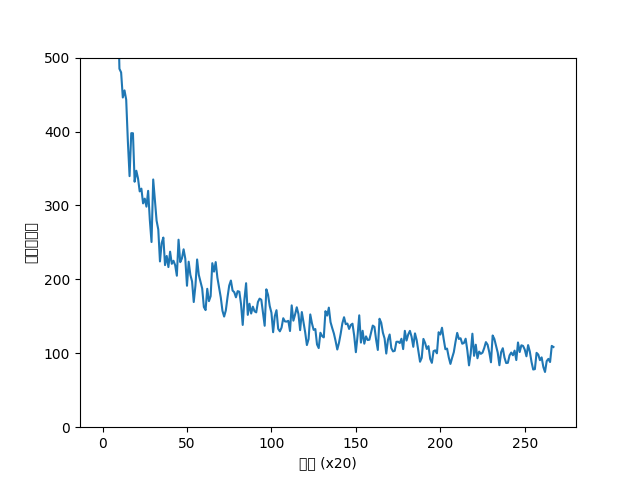
model.save_params()이제 이대로 학습을 수행해보자.


처음에는 나올 수 있는 단어의 가능성을 10000개 정도 생각했지만, 갈수록 그 수가 줄어드는 것을 확인할 수 있었다.
결과 그래프는 아래와 같다.
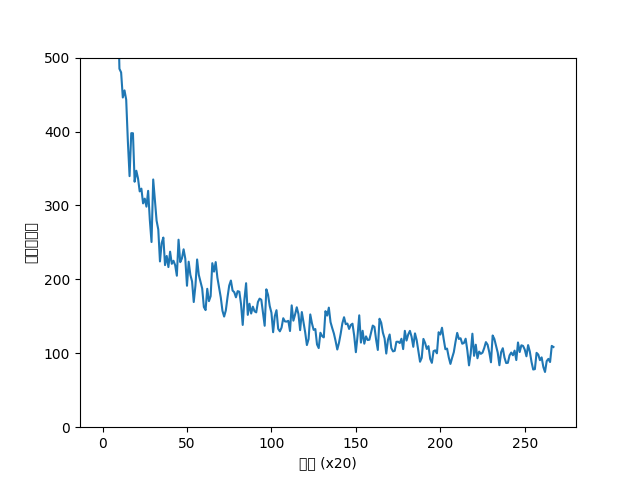
학습 결과, 테스트 퍼플렉서티가 134정도 되었다.
이는 우리 모델이 다음에 나올 단어의 후보를 134개 정도까지 줄였다는 뜻이 된다.
그러면 134라는 값이 과연 좋은 값일까?
2017년 기준의 연구에서는 PTB 데이터셋의 퍼플렉서티가 60을 밑돌고 있다.
이 RNNLM을 추가로 개선해보자.
RNNLM 추가 개선
이번 절에서는 다음 세가지 추가 개선을 수행할 것이다.
- LSTM 계층 다층화
- 드롭아웃에 의한 과대적합 억제
- 가중치 공유LSTM 계층 다층화우리는 지금까지 LSTM을 1층으로 사용하고 있었다.
RNNLM으로 보다 더 정확한 모델을 만들고자 한다면, 층 수를 늘리는 것을 고려할 수 있다.
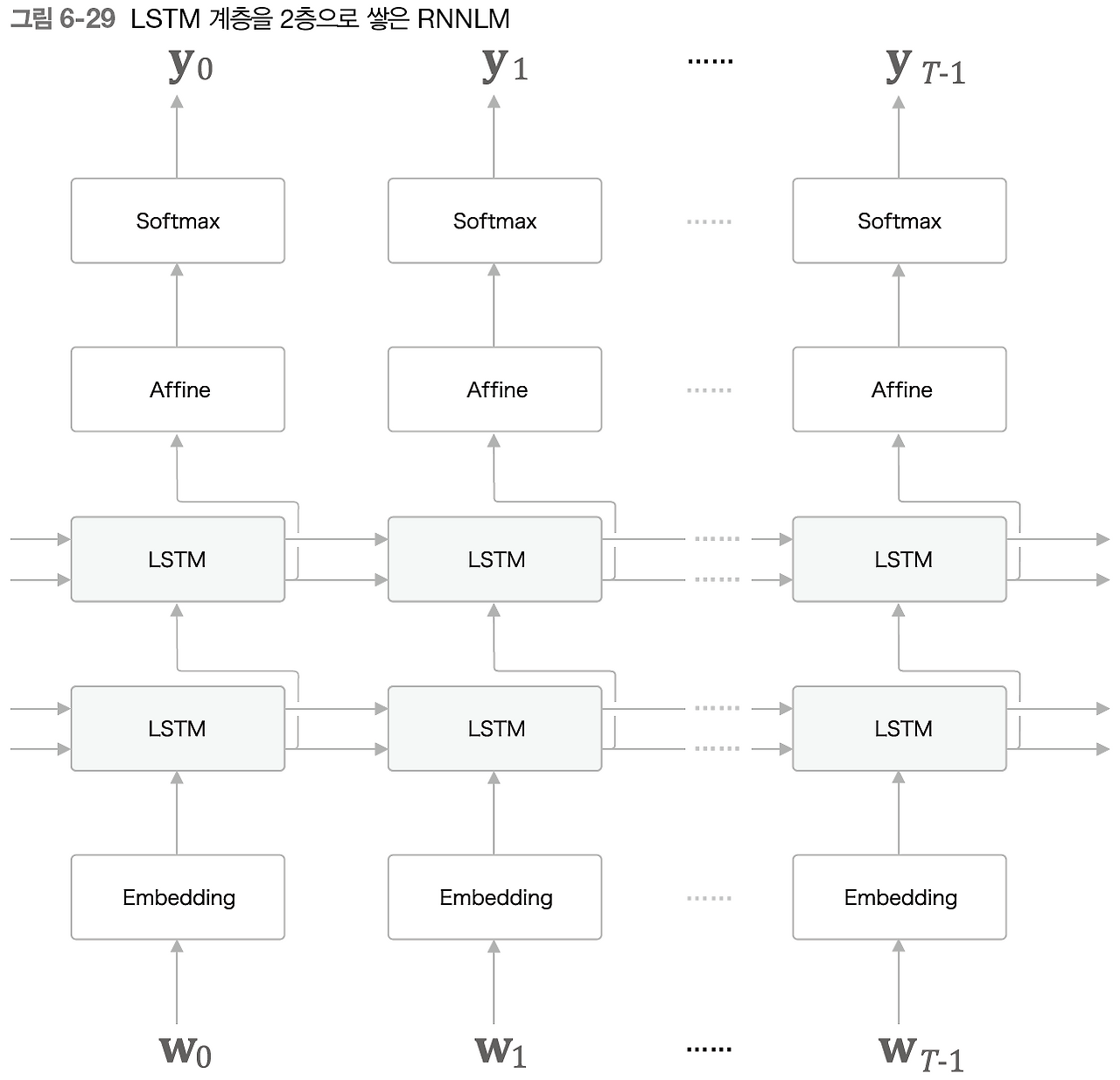
파라미터의 수가 많아지면, 학습하는데 오랜 시간이 걸리지만 표현력이 상승한다.
또한 데이터의 수에 비해 파라미터의 수가 많아지면 오버피팅 문제도 발생할 수 있기 때문에, 현재 데이터 수에 맞는 레이어 수를 조정하는 것이 좋다.
일반적으로 PTB 데이터셋의 언어 모델에서는 LSTM의 층 수를 2~4층으로 하는게 좋다고 알려져 있다.
드롭아웃에 의한 과대적합 억제
위에서 설명했듯, LSTM을 다층화하여 시계열 데이터의 복잡한 의존 관계를 학습할 수 있다.
하지만 이렇게 다층화를 하게되면, 주어진 데이터에만 표현력이 올라가는 "과대적합"이 발생할 수 있다.
게다가 RNN은 일반적인 피드포워드 신경망보다 쉽게 과대적합을 일으키기 때문에, 이를 개선하고자 하는 연구가 진행중이다.
일단 과대적합하면 떠오르는 방법은 이것들이 있었다.
- 배치 정규화
- 가중치 감소
- 드롭아웃
이번에는 드롭아웃을 적용해 우리 모델을 개선해보자.

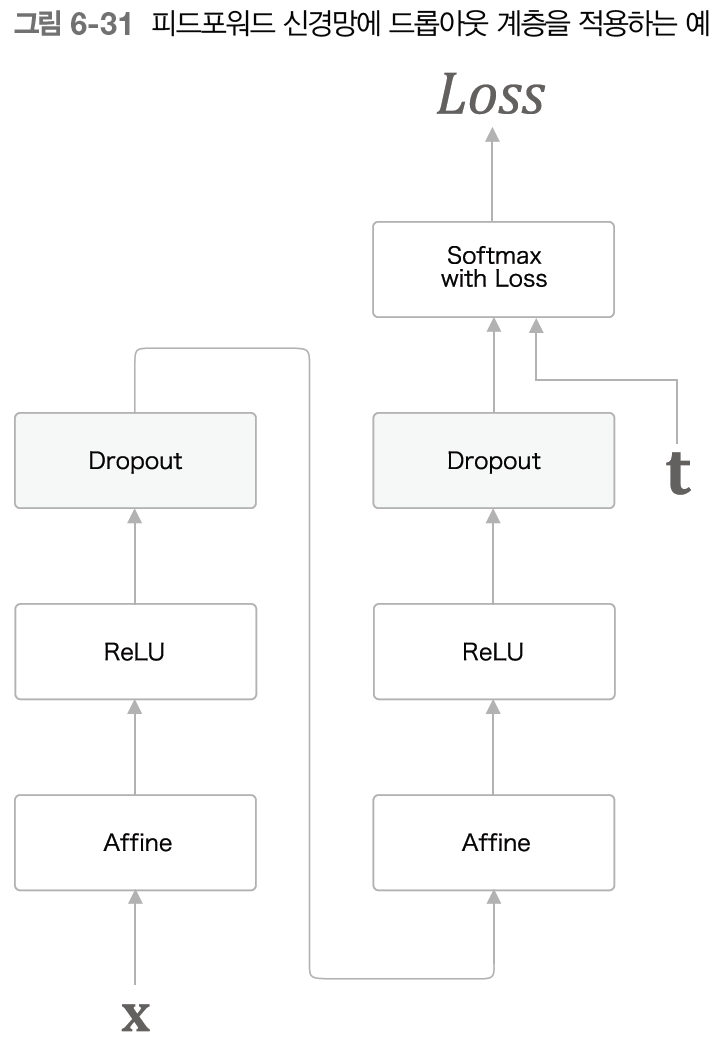
우리는 앞서 드롭아웃 계층을 구현해봤는데, 그때 우리는 드롭아웃 계층을 활성화 함수 뒤에 삽입하는 방식으로 구현을 수행했다.
[밑바닥부터 시작하는 딥러닝] 학습 관련 기술들
본 내용은 밑바닥부터 시작하는 딥러닝 1도서를 참고하여 작성되었습니다. 밑바닥부터 시작하는 딥러닝 1 - 예스24딥러닝 분야 부동의 베스트셀러!머리로 이해하고 손으로 익히는 가장 쉬운 딥
dev.go-gradually.me
RNN을 사용한 모델에서는 드롭아웃 계층을 어디에 삽입해야 할까?
- 시계열 셀 사이
- TimeRNN 레이어 사이
일단 첫번째 방법은 그다지 좋은 방법이 아니다.

RNN에서 시계열 방향으로 드롭아웃을 넣어버리면, 학습 시 시간이 흐름에 따라 정보가 "사라질 수" 있다.
즉, 흐르는 시간에 비례해 드롭아웃에 의한 노이즈가 축적된다.
그러니 두번째 안을 고려해보자.

이렇게 적용하면 시간 방향으로 아무리 진행해도 정보를 잃지 않는다.
드롭아웃이 시간축과는 독립적으로 깊이 방향(상하 방향)에만 영향을 주는 것이다.
지금까지 이야기한 것처럼, '일반적인 드롭아웃'은 시간 방향에는 적합하지 않다.
그러나 최근 연구에는 RNN의 시간 방향 정규화를 목표로 하는 방법이 다양하게 제안되고 있다.
대표적 예로 Variational Dropout은 깊이 방향은 물론 시간 방향에도 이용할 수 있어서 언어 모델의 정확도를 한층 더 향상시킬 수 있다.
그 구조는 아래와 같은데, 같은 계층에 속한 드롭아웃들은 같은 마스크(mask)를 공유한다.

여기서 말하는 '마스크'란 데이터의 통과/차단을 결정하는 이진 형태의 무작위 패턴이다.
같은 계층의 드롭아웃끼리 마스크를 공유함으로써 마스크가 '고정'되고, 그 결과 정보를 잃게 되는 방법도 '고정'된다.
따라서 일반적인 드롭아웃 때와 달리 정보가 지수적으로 손실되는 사태를 피할 수 있다.
가중치 공유
언어 모델을 개선하는 아주 간단한 트릭 중 가중치 공유(Weight tying)가 있다.
이를 직역하면 '가중치를 연결한다'이지만, 여기서는 가중치를 공유하는 효과를 준다.
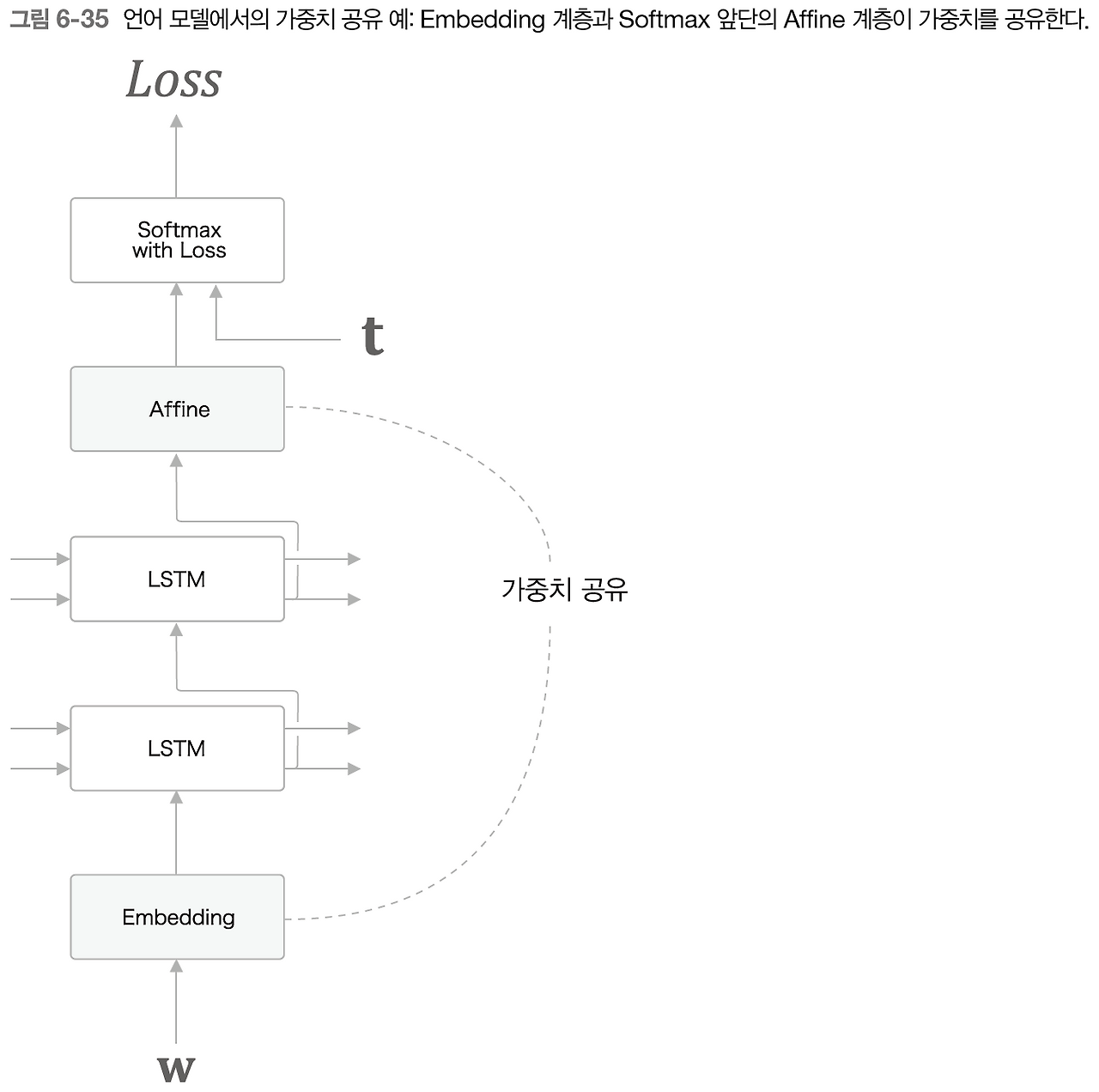
위 그림처럼 Embedding 계층의 가중치와 Affine 계층의 가중치를 연결하는 기법이 가중치 공유이다.
가중치를 줄이는 것이 오히려 "단어의 표현력"을 줄이지 않나? 라는 의문이 들 수 있는데,
입력 임베딩과 출력 분포가 동일한 의미 공간에 놓여야 한다는 강한 가정이 자연스럽고 유용하기 때문에 효과를 보는 경우이다.
각 계층의 역할을 다시 생각해보자.
- 입력 임베딩: 단어를 고차원 one-hot 벡터에서 의미 있는 저차원 공간으로 매핑 → 문맥을 이해할 수 있게 함.
- 출력 가중치(softmax matrix): 은닉 상태를 다시 어휘 분포로 매핑 → 어떤 단어가 나올 확률을 예측.
즉, 문맥 상의 대칭성이 있기 때문에, 양쪽의 계층을 대칭으로 만드는 것이다.
그럼 가중치 공유를 구현 관점에서 생각해보자.
어휘 수를 V로, LSTM의 은닉 상태의 차원의 수를 H라고 해보자.
그러면 Embedding 계층의 가중치는 형상이 VxH이며, Affine 계층의 가중치 형상은 HxV가 된다.
이때 가중치 공유를 적용하려면 Embedding 계층의 가중치를 전치하여 Affine 계층의 가중치로 설정하면 된다.
개선된 RNNLM 구현
이제 전체 아키텍처를 그려보자.
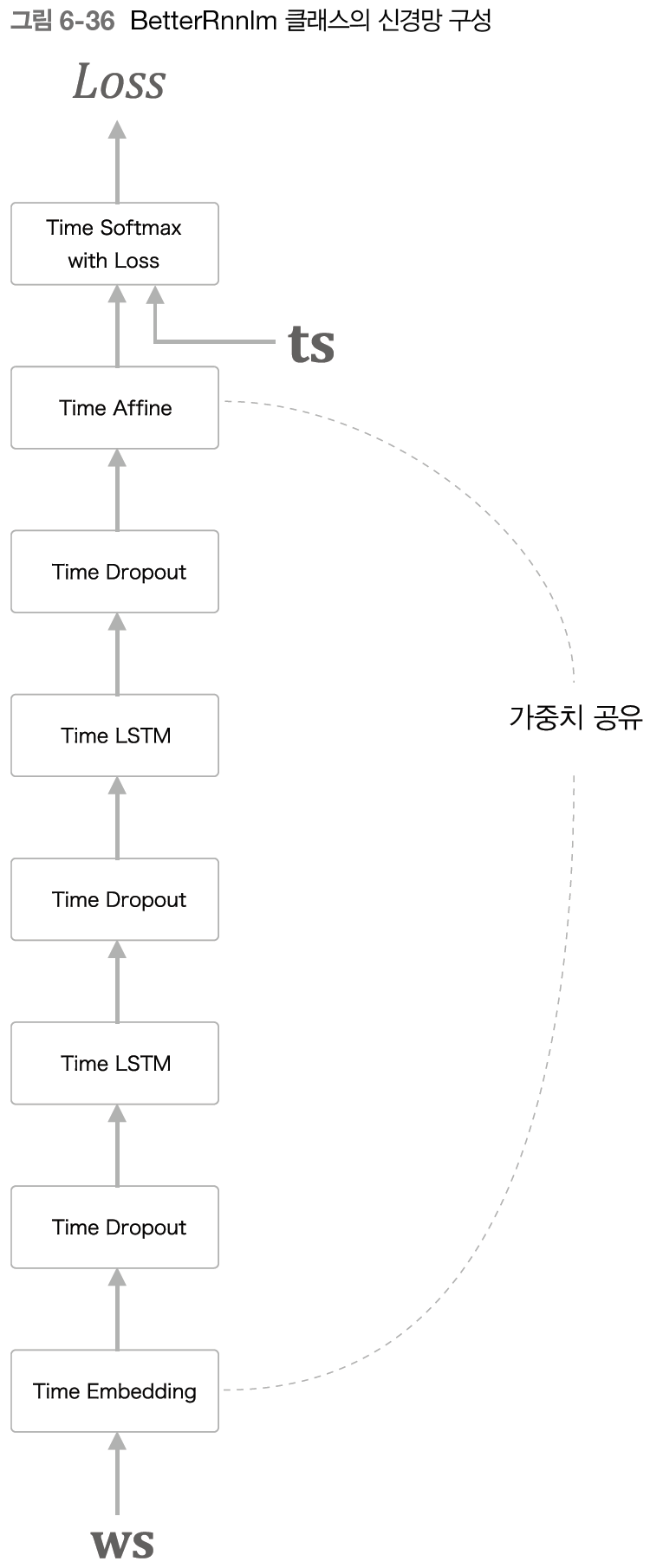
그림에서 보듯, 여기에서의 개선점은 다음 세가지이다.
- LSTM 계층의 다층화(여기에서는 2층)
- 드롭아웃 사용(깊이 방향으로만 적용)
- 가중치 공유
이제 이 세가지 개선점을 공유한 BetterRnnlm을 구현한다.
import sys
sys.path.append('..')
from common.time_layers import *
from common.np import *
from common.base_model import BaseModel
import pickle
class BetterRnnlm(BaseModel):
def __init__(self, vocab_size=10000, wordvec_size=650, hidden_size=650, dropout_ratio=0.5):
V, D, H = vocab_size, wordvec_size, hidden_size
rn = np.random.randn
embed_W = (rn(V, D)/ 100).astype('f')
lstm_Wx1 = (rn(D, 4*H)/ np.sqrt(D)).astype('f')
lstm_Wh1 = (rn(H, 4*H)/ np.sqrt(H)).astype('f')
lstm_b1 = np.zeros(4*H).astype('f')
lstm_Wx2 = (rn(H, 4 * H) / np.sqrt(D)).astype('f')
lstm_Wh2 = (rn(H, 4 * H) / np.sqrt(H)).astype('f')
lstm_b2 = np.zeros(4 * H).astype('f')
affine_b = np.zeros(V).astype('f')
self.layers = [
TimeEmbedding(embed_W),
TimeDropout(dropout_ratio),
TimeLSTM(lstm_Wx1, lstm_Wh1, lstm_b1, stateful=True),
TimeDropout(dropout_ratio),
TimeLSTM(lstm_Wx2, lstm_Wh2, lstm_b2, stateful=True),
TimeDropout(dropout_ratio),
TimeAffine(embed_W.T, affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss()
self.lstm_layers = [self.layers[2], self.layers[4]]
self.drop_layers = [self.layers[1], self.layers[3], self.layers[5]]
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self, xs, train_flg=False):
for layer in self.drop_layers:
layer.train_flg = train_flg
for layer in self.layers:
xs = layer.forward(xs)
return xs
def forward(self, xs, ts, train_flg=True):
score = self.predict(xs, train_flg)
loss = self.loss_layer.forward(score, ts)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
def reset_state(self):
for layer in self.lstm_layers:
layer.reset_state()다음은 이 개선된 BetterRnnlm 클래스를 학습시킬 차례이다.
하지만 그 전에 지금부터 수행하는 학습 코드에 한가지 궁리를 더해보자.
매 에폭에서 검증 데이터로 퍼플렉서티를 평가하고, 그 값이 나빠졌을 경우 학습률을 낮춰볼까?
이 기술은 실전에서 자주 쓰이며, 더 좋은 결과로 이어지는 경우가 많다.
참고로 이 구현은 PyTorch언어 모델의 구현 예를 참고했다.
import sys
sys.path.append('..')
from common import config
config.GPU = True
from common.optimizer import SGD
from common.trainer import RnnlmTrainer
from common.util import eval_perplexity
from dataset import ptb
from better_rnnlm import BetterRnnlm
# 하이퍼파라미터 설정
batch_size = 20
wordvec_size = 650
hidden_size = 650
time_size = 35
lr = 20
max_epoch = 40
max_grad = 0.25
dropout = 0.5
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_test, _, _ = ptb.load_data('test')
corpus_val, _, _ = ptb.load_data('val')
vocab_size = len(word_to_id)
xs = corpus[:-1]
ts = corpus[1:]
model = BetterRnnlm(vocab_size, wordvec_size, hidden_size, dropout)
optimizer = SGD(lr)
trainer = RnnlmTrainer(model, optimizer)
best_ppl = float('inf')
for epoch in range(max_epoch):
trainer.fit(xs, ts, max_epoch=1, batch_size=batch_size, time_size=time_size, max_grad=max_grad)
model.reset_state()
ppl = eval_perplexity(model, corpus_test)
print('epoch: ', epoch, ' test perplexity: ', ppl)
if best_ppl > ppl:
best_ppl = ppl
model.save_params()
else:
lr /= 4.0
optimizer.lr = lr
model.reset_state()
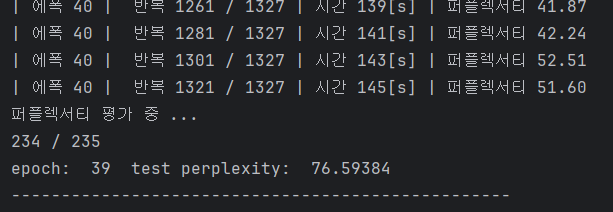
print('-'*50)
이번 장에서 배운 것
- 단순한 RNN의 학습에서는 기울기 소실과 기울기 폭발이 문제가 된다.
- 기울기 폭발에는 기울기 클리핑, 기울기 소실에는 게이트가 추가된 RNN(LSTM, GRU 등)이 효과적이다.
- LSTM에는 input게이트, forget 게이트, output 게이트 등 3개의 게이트가 있다.
- 게이트에는 전용 가중치가 있으며, 시그모이드 함수를 사용하여 0.0~1.0 사이의 실수를 출력한다.
- 언어 모델 개선에는 LSTM 계층 다층화, 드롭아웃, 가중치 공유 등의 기법이 효과적이다.
- RNN의 정규화는 중요한 주제이며, 드롭아웃 기반의 다양한 기법이 제안되고 있다.
'AI Repository > 기초 딥러닝' 카테고리의 다른 글
| [밑바닥부터 시작하는 딥러닝] 어텐션 메커니즘 (0) | 2025.08.22 |
|---|---|
| [밑바닥부터 시작하는 딥러닝] seq2seq, Encoder-Decoder (0) | 2025.08.20 |
| MatMul 노드(행렬곱)의 역전파 (0) | 2025.08.16 |
| [밑바닥부터 시작하는 딥러닝] RNN (0) | 2025.08.15 |
| [밑바닥부터 시작하는 딥러닝] word2vec (0) | 2025.08.13 |