어떤 데이터의 확률밀도함수 p(x)가 있다고 하자.
이 함수를 정확히 알 수 없어서 이 함수를 근사적으로 추정한 확률밀도함수 q(x)를 사용한다고 가정하자.
그러면 실제 분포인 p(x)로 얻을 수 있는 정보량과 근사적 분포인 q(x)로 얻을 수 있는 정보량은 다를 것이다.
이때 둘 사이의 평균 정보량이 얼마나 차이가 나는지 계산한 것을 상대 엔트로피(relative entropy) 또는 KL 발산(Kullback-Leibler divergence)이라고 하며, 다음과 같이 정의한다.

- 여기서 p(x)||q(x)는 p(x)를 기준으로 q(x)를 비교한다는 뜻이다.
- 첫 번째 항은 근사 분포인 q(x)의 정보량을 실제 분포를 사용해 기댓값을 계산한 것(크로스 엔트로피)이다.
- 두번째 항은 실제 분포 p(x)의 평균 정보량(엔트로피)이다.
KL 발산은 두 확률분포의 엔트로피 차이를 나타낸다.
또한 KL 발산은 두 확률분포가 얼마나 유사한지 '거리'를 측정하는 도구로도 쓰인다.
실제로 KL 발산은 거리의 척도(metric) 특성 4가지 중 3가지만을 만족하고 대칭성을 만족하지 못하기 때문에 준(semi) 거리 척도라고 한다.
참고: 거리 척도 특성이란, "거리"라고 말할 수 있게 되기 위한 기준을 의미한다.
이 특성에는 다음 4가지가 존재한다.
비음성: d(x, y) >= 0
동일성: d(x,y)=0 이면 x=y이고, 그 역도 성립한다.
대칭성: d(x, y) = d(y, x)
삼각부등식 d(x, z) <= d(x, y) + d(y, z)
KL 발산의 정의에 의하면 몇 가지 특징을 추출할 수 있다.
우선, KL 발산은 비대칭 함수이다.

또한, 항상 아래 식을 만족한다.

두번째 식은 -log 함수가 컨벡스(convex, 볼록)함수임을 이용해 증명할 수 있다.
컨벡스 함수(볼록함수) f(x)에 대해서는 다음과 같은 젠슨 부등식이 성립한다.

젠슨 부등식에서, 만약 함수 f가 오목함수라면, 부등호가 반대가 된다.
이 정보를 이용해, KL 발산 식을 살짝 변형해보자.

라고 정의해보자. 따라서
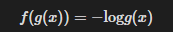
이렇다고 하면
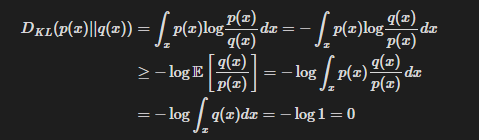
이 되는 것을 알 수 있다.
원본 확률밀도함수의 추정
p(x)와 q(x)가 각각 평균이 mu_p, mu_q, 공분산이 P_p, P_q 인 n차원 가우시안 분포(다변량 정규분포)라면 KL 발산은 다음과 같이 계산된다.

공분산(covariance)이 뭔지 모른다면, 두 확률변수가 함께 얼마나, 어떤 방향으로 변하는지를 수치로 나타낸 값이라고 알아두면 된다.
Cov(x, x) = var(x)이다.
det는 행렬식을 이야기한다.
실제 데이터의 분포가 p(x)로 주어지고, 이를 q(x)로 추정하고자 할 때 해당 데이터 집합에서 p(x)는 고정이므로(물론 알지는 못하지만) p(x)와 유사한 q(x)를 계산하는 것을 다음과 같이 생각할 수 있다.

즉, 데이터 집합이 주어졌을 때 미지의 p(x)와 유사한 q(x)는 크로스 엔트로피 H(p, q)를 최소로 만드는 확률밀도함수이다.
argmin은 우항을 최소로 만드는 q를 반환하는 함수라고 생각하면 된다.
배열의 최솟값의 인덱스를 찾는다고 생각하면 좋다.
본 내용은 수학으로 풀어보는 강화학습 원리와 알고리즘 도서를 참고하여 작성되었습니다.
수학으로 풀어보는 강화학습 원리와 알고리즘 - 예스24
코딩하면서 알고리즘이 유도된 과정이 궁금하다면 이 책을 선택하기 바랍니다!이 책은 딥러닝이나 강화학습 예제를 코딩하면서 그 배경 알고리즘의 유도 과정을 궁금해하는 사람을 위한 책이
www.yes24.com
'AI Repository > 기초 통계학' 카테고리의 다른 글
| [정보 이론] Estimator - MLE, MAP, 수학적 추정 (0) | 2025.09.24 |
|---|---|
| [정보 이론] 정보량, 엔트로피와 Cross Entropy의 정의 (0) | 2025.09.24 |
| [개발자를 위한 필수 수학] 로지스틱 회귀와 분류 (0) | 2025.08.04 |
| [개발자를 위한 필수 수학] 선형회귀 (2) | 2025.07.31 |
| [개발자를 위한 필수 수학] 추론통계 (1) | 2025.07.24 |