딥러닝을 학습하며 "크로스 엔트로피 오차"를 아무렇지 않게 사용하고 있었다.
그런데 최근 논문을 탐색하면서, "크로스 엔트로피"라는 용어의 정의를 생각보다 엄밀하게 규정해두지 않아 개념들이 잘 이해가 가지 않았다.
따라서 다음과 같이 엔트로피의 엄밀한 정의에 대해 서술한다.
항상 일어나는 사건은 새로울 것이 없으므로 여기에서 얻을 수 있는 정보의 양은 매우 적다고 봐도 된다.
또한 잘 일어날 것 같지 않는 사건에서는 빈번하게 일어나는 사건에서보다 얻을 수 있는 정보의 양이 더 많다고 봐도 될 것이다.
따라서 정보량은 사건의 발생 빈도의 영향을 받으므로, 확률적인 속성을 가지고 있고, 확률함수로 나타내는 것이 자연스러워진다.
이를 반영해 랜덤벡터 x의 정보량 h(x)를 다음과 같이 정의한다.

여기서 p(x)는 x의 확률밀도함수다.
p(x)값이 0에 가까워질수록, 즉 사건의 빈도수가 작을수록 정보량은 많아지고
p(x)값이 커질수록, 즉 사건의 빈도수가 클수록 정보량은 적어진다.
이는 잘 발생하는 사건에서는 적은 정보를 획득하고, 자주 발생하지 않는 사건에 대해서는 많은 정보를 획득하므로, 정보의 희귀성과 그 의미를 잘 표현했다고 할 수 있다.
엔트로피(entropy)는 정보량의 기댓값으로 정의하며 다음과 같다.

즉, 엔트로피는 확률밀도 p(x)를 가중치로 해서 가중평균을 구하는 것이다.
각 확률에 담긴 정보량과 그 확률의 크기를 가중치로 해서, 분포 전체에서 평균적으로 얻는 정보량을 취하는 것이다.
예를 들어 x를 스칼라 랜덤 변수라고 할 때 p(x)가 다음과 같이 평균이 mu이고 분산이 sigma^2인 가우시안 분포함수라면

엔트로피는 다음과 같이 된다.
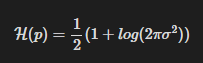
이 경우 엔트로피는 분산에만 영향을 받으며, 분산이 커질수록 증가함을 알 수 있다.
분산이 클수록 사건의 무작위성이 커지고 특정 사건의 발생 빈도수가 작아지기 때문에 정보량이 증가한다고 볼 수 있다.
참고로 물리 시스템에서도 엔트로피가 증가할수록 무작위성 또는 무질서의 정도가 증가한다고 해석한다.
확률밀도함수 q(x) 의 정보량을 확률밀도함수 p(x)의 관점에서 기댓값으로 표현한 것을 p(x)와 q(x)의 Cross Entropy 라고 하며, 다음과 같이 정의한다.
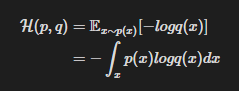
정보량의 과학적 개념은 '내가 아는 어떤 것의 총량'이 아니라 '어떤 것의 가능한 대안의 수 또는 모든 경우의 수의 총량'을 의미한다.
예를 들어 주사위를 던지면 6가지 숫자 중에서 하나가 나오므로 정보량은 6이다.
어떤 사람의 생일은 모르면 365(366)개의 가능성이 존재하기 때문에, 만약 그사람의 생일을 안다면 나의 정보량은 365이다.
어떤 사건의 경우의 수가 많다는 것은 곧 특정한 사건이 일어날 가능성이 더 희박하다는 이야기이므로 정보량은 확률적인 속성을 가지고 있다고 볼 수 있다.
본 내용은 수학으로 풀어보는 강화학습 원리와 알고리즘 도서를 참고하여 작성되었습니다.
수학으로 풀어보는 강화학습 원리와 알고리즘 - 예스24
코딩하면서 알고리즘이 유도된 과정이 궁금하다면 이 책을 선택하기 바랍니다!이 책은 딥러닝이나 강화학습 예제를 코딩하면서 그 배경 알고리즘의 유도 과정을 궁금해하는 사람을 위한 책이
www.yes24.com
'AI Repository > 기초 통계학' 카테고리의 다른 글
| [정보 이론] Estimator - MLE, MAP, 수학적 추정 (0) | 2025.09.24 |
|---|---|
| [정보 이론] KL Divergence (KL 발산) - 크로스 엔트로피를 쓰는 이유 (0) | 2025.09.24 |
| [개발자를 위한 필수 수학] 로지스틱 회귀와 분류 (0) | 2025.08.04 |
| [개발자를 위한 필수 수학] 선형회귀 (2) | 2025.07.31 |
| [개발자를 위한 필수 수학] 추론통계 (1) | 2025.07.24 |