우리가 기존에 알고있던 DQN은 Q 함수를 하나의 신경망으로 근사하는 "정책 외 알고리즘"이다.
즉, DQN은 행동을 했을 때 얻을 수 있는 기대 보상을 기준으로 판단하는 알고리즘이다.

QN이 예측한 Q value들은 특정 정책에 따라 다음 동작을 선택하는데 쓰인다.
동작을 선택하는 정책은 다양한데, 현재 우리는 입실론-그리디 정책 정도만 학습했다.
그 외에도 Q value들에 소프트맥스 층을 적용해서 하나의 동작을 선택하는 등 다양한 정책이 가능하다.
그런데 신경망과 정책을 따로 두고 동작을 선택하는 대신, 신경망이 직접 동작을 선택하도록 훈련하면 어떨까?
이 경우 신경망은 정책 함수(policy function)의 역할을 한다.
이런 신경망을 정책 신경망, 줄여서 정책망(policy network)이라고 부른다.
지금부터 이 정책망을 구현하는 방법에 대해 알아보자.
신경망을 이용한 정책 함수 구현
이번 글에서는 가치 함수 V_pi 또는 Q가 아니라 정책 함수 pi(s)를 근사하는 학습 알고리즘들을 소개한다.
즉, 동작 가치들을 출력하도록 신경망을 훈련하지 않고, 동작 자체를 출력하도록 신경망을 훈련한다.
정책 함수로서의 신경망
DQN과는 달리 정책망은 주어진 상태에서 취해야 할 동작을 명시적으로 말해준다.
즉, 또다른 동작 결정 과정은 필요하지 않다.
그냥 정책망이 산출한 확률분포 P(A|S)에 대해 무작위로 표집을 실행하면 동작이 나온다.
기대 보상이 큰 동작일수록 확률이 높으므로, 무작위 표집을 적용하면 기대 보상이 큰 동작들이 더 자주 선택된다.
즉, 탐험과 최선의 선택조차 신경망이 직접 판단하도록 만든 것이다.
이러한 부류의 알고리즘들을 통칭해서 정책 기울기 방법(policy gradient method; 또는 정책 경사법)이라고 부른다.
이러한 방식은 DQN과 이러한 것들이 다르다.
- 입실론-탐욕 정책과 같은 동작 선택 정책을 따로 둘 필요가 없다.
- 학습의 안정성을 위해 추가적인 기법들을 적용하기가 한결 더 수월하다.
- Target Network, ER 등의 도입을 좀 더 적용하기가 쉽다.
확률적 정책 기울기 방법
구체적인 정책 기울기 방법은 여러 가지인데, 앞에서 설명한 것은 확률적 정책 기울기(stochastic policy gradient) 방법에 해당한다.
확률적 정책 기울기 방법에서는 신경망이 동작 선택을 위한 확률분포에 해당하는 하나의 벡터를 산출한다.
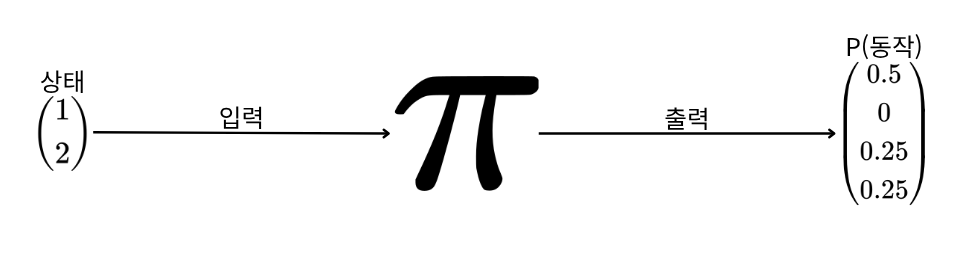
위 그림에서는 1, 2라는 상태를 정책망에 입력했을 때, 이에 정책망은 상,하,좌,우를 각각 선택할 확률을 출력한다.
환경이 시불변(stationary)이라면, 즉 상태들과 보상들의 분포가 고정되어 있다면, 그리고 결정론적인 전략을 사용한다면, 정책 함수가 산출하는 확률분포들은 점차 하나의 퇴화분포(degenerate probability distribution)로 수렴하게 된다.
퇴화 분포란, 모든 확률질량에 동일한 하나의 결과가 배정된 확률분포를 말한다.
이를 그림으로 표현하면 아래와 같다.

이 경우 퇴화 분포는 한 항목의 확률만 1이고 나머지는 모두 확률이 0인 확률분포이다.
전체 훈련 과정의 초반부에서는 적극적인 탐험이 필요하므로, 정책망이 상당히 균등한 확률분포를 산출하는 것이 좋다.
그러나 어느 정도 훈련이 진행된 후에는 확률분포가 최선의 동작이 더 자주 선택되는 쪽으로 수렴해야 한다.
주어진 상태에서 최선의 동작이 단 하나인 경우에는 정책망이 퇴화분포로 수렴해야 할 것이다.
가치가 비슷한 동작이 두 개 있다면, 모드가 두 개인 확률분포가 나와야 할 것이다.
확률분포의 모드는 그냥 '봉우리', 즉 확률분포를 그래프로 그렸을 때 불쑥 솟은 부분의 또다른 이름이다.
탐험
강화학습에서 탐험이 없다면, 좀 더 나은 정책을 학습하긴 어려울 것이다.
확률적 정책 기울기 방법과 대조되는 정책 기울기 방법으로 결정론적 정책 기울기 방법이 있다.
이 방법은 항상 에이전트가 취할 하나의 동작을 산출한다.
여기에는 확률적 요소가 없으므로, 만일 에이전트가 항상 이 정책 함수만 따른다면 탐험이 부족해진다.
또한, 이산적인 동작 집합에 따른 결정론적 정책 함수의 출력은 이산적인 값들이므로, 미분이 필요한 심층 학습 기법을 적용하기 어렵다.
따라서 이번 장에서는 확률적 정책 기울기 방법에 초점을 둔다.
사실 모형에 어느 정도의 불확실성을 도입하는(이를테면 확률분포를 이용해서) 것은 일반적으로 좋은 일이다.
좋은 동작의 강화: 정책 기울기 알고리즘
앞서 우리는 정책 함수와 그 정책함수를 신경망으로 근사할 수 있다는 점을 이야기했다.
이제 본격적으로 이런 알고리즘을 실제로 구현하고 훈련(최적화)하는 방법을 살펴보자.
목적함수 정의
기억하겠지만, 신경망을 훈련하려면 신경망의 가중치(매개변수)들에 대해 미분 가능한 목적함수가 필요하다.
앞서 DQN에선 MSE를 사용했다.
그렇다면 주어진 상태에서 가능한 동작들에 관한 확률분포 P(A|S)를 산출하는 정책망은 어떤 식으로 훈련해야 할까?
동작을 취한 후 관측된 보상들을 P(A|S)의 갱신에 대응시키는 어떤 자명한 방법은 없다.
DQN의 훈련이 지도학습 문제의 경우와 그리 다르지 않았던 것은 Q 신경망이 예측 Q Value들의 벡터를 산출한다는 점과 정해진 공식에 따라 Target Q value 벡터를 산출할 수 있다는 점 덕분이었다.
예측값과 목푯값만 있으면, 통상적인 DL 방법에 따라 오차를 최소화하는 식으로 신경망을 훈련할 수 있다.
반면 정책망은 동작(의 확률)들을 직접 예측하며, 최대 가치로 이어지는 바람직한 '목표'동작들의 벡터를 구하는 공식은 없다.
우리가 아는 것은 그냥 동작이 긍정적 보상 또는 부정적 보상으로 이어지는지 뿐이다.
사실 최선의 동작은 암묵적으로 가치 함수에 의존하지만, 애초에 정책망 접근 방식은 그런 동작 가치들을 직접 계산하지 않아도 동작을 선택할 수 있도록 고안된 것이다.
그럼 정책망을 훈련하는 방법을 구체적인 예제를 통해서 살펴보자.
우선, 다음과 같이 표기법을 정리하겠다.
- π: 정책망
- θ: 정책망의 매개변수를 담은 벡터
- π_θ: 매개변수가 담긴 정책망을 명시적으로 표현
정책망의 순전파 과정에서 매개변수 벡터 θ는 고정된다.
변수(독립변수)는 정책망에 입력되는 데이터(즉, 게임의 상태)이지 θ가 아니다.
이 점을 나타내기 위해 θ를 아래첨자로 두어서 정책망을 π_θ로 표기했다.
함수에서 독립변수와 종속변수가 무엇인지, 상수가 무엇인지를 정의하는 것이 매우 중요함을 잊지 말자.
아직 훈련되지 않은 정책망 π_θ에 Gridworld의 초기 게임 상태 s를 입력해서 정책망을 실행하면 π_θ(s)가 평가된다.
이 함수는 네 가지 동작에 관한 확률분포를 돌려준다.

Gridworld같은 episodic한 게임들에선 게임의 한 에피소드의 시작과 끝이 명확히 정의된다.
하나의 에피소드는 시작 상태에서 종료 상태에 도달할 때까지의 (상태, 동작, 보상) 튜플들의 sequence로 간주할 수 있다.
그래서 이 하나의 에피소드 ε를 다음과 같이 표기한다.
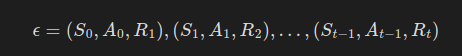
이 순차열에서 각 튜플('경험')은 Gridworld 게임의 한 시간 단계에 해당한다.
시간 t에서 에피소드의 끝에 도달했을 때 이 에피소드 시퀀스는 에피소드 전체의 역사를 담은 상태가 된다.
정책망을 따라 동작을 선택해서 단 세 번의 이동만에 목표에 도달했다고 하면, 에피소드는 다음과 같은 모습이 될 것이다.

- 참고로 행동은 네 가지 동작을 0에서 3까지의 정수로 표현했다.
- 상태는 64차원 벡터이지만, 간결함을 위해 S 기호로만 표기했다.
이 에피소드에서 무엇을 배울 수 있을까?
마지막 튜플의 보상이 +10이라는 것은 에이전트가 게임에서 승리했음을 뜻한다.(게임이 그렇게 설계되어 있다)
따라서 이 에피소드의 동작들은 어느정도 "좋은" 동작들일 것이다.
따라서, 이와 비슷한 상태들에서 정책망이 이 에피소드의 동작들에 좀 더 높은 확률에 부여하도록 훈련해야 한다.
다른 말로 하면, 긍정적인 보상으로 이어지는 동작들을 강화해야 한다.
에이전트가 게임에서 패배한(마지막 보상이 -10인) 에피소드에서 무엇을 배울 수 있는지는 이번 장에서 나중에 이야기하겠다.
일단 지금은 긍정적 강화에 집중하자.
동작 강화
정책망을 훈련하는 과정은 미래에 승리로 이어지는 동작들에 대해 좀 더 높은 확률을 배정하도록 정책망의 매개변수들을 조금씩 매끄럽게 갱신하는 과정이다.
한 가지 간단한 접근 방식은, [0,0,0,1]을 목표 동작 분포로 두고 경사 하강법을 실행해서 [0.25,0.25,0.25,0.25]가 [0,0,0,1]과 좀 더 가까워지게 만드는 것이다.
그러면 정책망은 다음 번에 예를 들어 [0.167,0.167,0.167,0.5]와 같은 확률분포를 산출할 것이다.

이는 지도학습 문제에서 흔히 쓰이는 방법과 비슷하다.
예를 들어 소프트맥스 기반 이미지분류에 이런 방법이 쓰이는데, 이미지 분류 과제에는 '정답'(이미지의 정확한 분류명)이 존재하며 각 예측 사이에 시간적인 연관 관계가 없다.
그러나 강화학습에서는 그렇지 않기 때문에 매개변수 갱신 과정을 좀 더 정교하게 만들어야 한다.
무엇보다도 각 갱신량이 작고 매끄러워야 한다.
이는 환경을 제대로 탐험하려면 동작 표집에 약간의 "불확실성"이 남아 있어야 하기 때문이다.
또한, 최근 동작들과 시간이 좀 지난 동작들이 갱신에 미치는 영향을 서로 다르게 설정할 수 있어야 한다.
이 두 문제는 표기법들을 마저 설명한 후 다시 살펴보겠다.
동작 확률분포를 산출하는 순전파 과정에서는 매개변수 벡터 θ가 고정되므로 정책망을 π_θ로 표기한다는 점을 기억할 것이다.

따라서 위 표기는,
- 어떤 상태 s에 대해,
- 고정된 정책망 매개변수 θ로
- 산출된 확률분포 π
를 의미한다.
하지만 이번에는(정책망을 훈련할 때는) 고정된 입력에 대해 매개변수 θ를 달리 두어서, 목적함수가 최적화되는 매개변수를 찾을 것이다.
그래서 아래와 같이 표기한다.
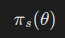
위 표기는
- 신경망의 파라미터 θ에 대해,
- 고정된 상태 s로
- 산출된 확률분포 π
를 의미한다.

동작 3(앞서 정의했다)을 강화하려면 위 확률이 증가하도록 정책망 매개변수 벡터 θ를 갱신해야 한다.
목적함수는 위 식을 최대화하려고 하지만, 이렇게 구현하면 PyTorch의 내장 최적화 모듈과 잘 맞지 않는다.
파이토치는 경사 "상승법"보단, 경사 "하강법"이 편하다.
따라서 위 식을 최대화하는 것이 아닌, 아래 식을 최소화하는 것으로 수식을 바꾼다.

이제부터, 동작을 지칭할 때 아래첨자(동작 번호)를 적지 않겠다.
문맥으로 구별해주길 바란다.
로그 우도
지금까지의 설명이 수학적으로는 정확하지만, 실제 구현을 위해서는 조금 수정이 필요하다.
- 확률은 0부터 1까지 사이의 실수로 정의되는데, 이는 부동소숫점의 정확도 표현에 어려움이 있다.
- 컴퓨터 연산은 곱셈보단 덧셈이 편한데, 그런 의미에서 log를 취하는 것은 효과가 좋다.
따라서 목적함수로 "음의 로그 우도"를 사용하도록 하자.

기여도 배정 문제
현재 우리의 목적함수는 에피소드의 모든 동작이 동일한 비중으로 매개변수들의 갱신에 영향을 끼친다.
하지만, 일반적으로는 목표에 도달하기 직전의 동작이 에피소드의 첫 동작보다 게임 승리에 더 많이 기여했다고 보아야 마땅하다.
체스 플레이 강화학습에서도 첫 수보다는 마지막 수의 기여도가 더 크다고 인정한다.
이처럼 과거의 동작들을 어느 정도나 중요시할 것인지 고민하는 문제를 기여도 배정(credit assignment)문제라 부른다.
DQN에서는 할인율 gamma를 통해 이를 달성했는데, 이를 우리의 목적함수(손실함수)에 대입할 수는 없을까?
손실함수를 다음과 같이 정의해보자.
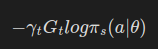
- 여기서 gamma_t는 할인 계수인데, 시간 단계에 따라 할인 계수가 달라져야 하므로 아래 첨자 t를 붙였다.
- G_t는 시간 t 단계에서의 "미래 보상"을 의미하는 수익이다. 이는 시간 단계 t에서 에피소드 끝까지 나아갔을 때 받을 전체 보상이다.

시간 단계 t에서의 할인 계수는 다음과 같이 정의된다.

이렇게 정의하면, 얼추 기여도 배정 문제를 해결 가능하다.
Gym 다루기
그럼 본격적으로 OpenAI Gym 환경(farama의 Gymnasium) 을 다뤄보자.
현재 강화학습 환경은 OpenAI에서 farama재단으로 이전하여, Gymnasium이라는 별도의 프로젝트를 제공하고 있다.
이 Gym 환경은 새로운 심층 강화학습 알고리즘을 구현했을 때, 성능을 평가하기 좋은 지표가 되어줄 것이다.
해당 프로젝트에는 다음과 같은 환경들이 존재한다.
- Algorithms(기본적인 알고리즘들)
- Atari(아타리 게임들)
- Box2D
- Classic control(고전적 제어 문제들)
- MuJoCo
- Robotics(로봇 제어 문제들)
- Toy text(간단한 텍스트 환경들)
안타깝게도 일부 환경은 사용 허가가 필요하거나 외부 의존 모듈을 따로 설치해야 해서 준비하는 데 시간이 좀 필요하다.
여기서는 별다른 준비 없이 바로 시험해 볼 수 있는 환경인 CartPole을 예로 들겠다.
CartPole

CartPole은 OpenAI의 고전적 제어 문제 범주에 속하는 환경으로, 목표는 간단하다.
위 사진에 보이는 막대(장대)가 쓰러지지 않게 하면 된다.
이를테면 손바닥 위에 펜을 세워보는 것을 상상할 수 있다.
환경의 상태는 다음 네가지의 4차원 벡터로 이루어져 있다.
- 카트 위치
- 카트 속도
- 막대 각도
- 막대 속도
각 시간 단계에서 막대가 쓰러지지 않으면 +1의 보상을 받는다.
따라서 보상을 최대화하려면 막대를 최대한 오랫동안 세워 두어야 한다.
Gym API
https://gymnasium.farama.org/introduction/basic_usage/
좋은 가이드는 위에 이미 존재하지만, 좀 더 "간단한" 사용법을 언급하겠다.
Gymnasium Documentation
A standard API for reinforcement learning and a diverse set of reference environments (formerly Gym)
gymnasium.farama.org
import gymnasium as gym
env = gym.make('CartPole-v0')위와 같은 코드로 환경 객체를 받아올 수 있다.
state1 = env.reset()위 코드로 환경을 초기화한다.
action = env.action_space.sample()
print(action)이 코드로 행동의 형식이 어떻게 이루어져 있는지 확인해볼 수 있다.
state, reward, done, info = env.step(action)주어진 환경에서 특정한 행동을 수행했을 때의 결과를 다음과 같이 받아올 수 있다.
CartPole과 관련된 자세한 정보는 해당 링크를 참고하자.
https://gymnasium.farama.org/environments/classic_control/cart_pole/
Gymnasium Documentation
A standard API for reinforcement learning and a diverse set of reference environments (formerly Gym)
gymnasium.farama.org
REINFORCE 알고리즘
지금까지 우리는 정책 기울기 알고리즘이 대략 어떤 것인지 파악했고, OpenAI Gym 환경을 다루는 기본적인 방법도 익혔다.
그럼 정책 기울기 알고리즘을 실제로 구현해보자.
앞에서 설명한 정책 기울기 방법은 나온 지 수십 년 된 REINFORCE 라는 한 알고리즘에 기초한 것이었다.
이 REINFORCE는 두문자어라서 영문 대문자로 표기해야 한다.
이제 이 REINFORCE 알고리즘을 실제로 구현해보자.
정책망 구축
우리는 다음과 같은 구조로 정책망을 구현할 것이다.
- 상태 벡터를 입력 받으면
- 가능한 동작들에 관한 (이산)확률분포를 산출한다.
정책망을 구현하고 나면, 강화학습 에이전트는 그 정책망의 확률분포에서 동작을 추출하고 실행하는 간단한 형태로 완성할 수 있다.
import gymnasium as gym
import numpy as np
import torch
l1 = 4
l2 = 150
l3 = 2
model = torch.nn.Sequential(
torch.nn.Linear(l1, l2),
torch.nn.LeakyReLU(),
torch.nn.Linear(l2, l3),
torch.nn.Softmax(dim=0),
)
learning_rate = 0.0009
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
에이전트와 환경의 상호작용
강화학습의 에이전트는 상태를 받고 하나의 동작을 산출한다.
지금 예에서 에이전트는 현재 상태를 정책망에 입력해서 현재 배개변수들과 상태를 조건으로 한 동작들의 조건부 확률분포 P(A|θ, S_t)를 얻는다.
여기서 대문자 A는 특정한 하나의 동작이 아니라 주어진 상태에서 취할 수 있는 모든 동작의 집합임에 주의하자.
지금 예에서 정책망의 출력은 2차원 벡터이다.
이 벡터의 첫 성분은 카트를 왼쪽으로 이동하는 동작(동작 0)의 확률이고 둘째 성분은 오른쪽으로 이동하는 동작(동작 1)의 확률이다.
코드에서 이 출력 벡터를 pred라는 변수에 담도록 하자.
pred = model(torch.from_numpy(state1).float())
action = np.random.choice(np.array([0, 1]), p=pred.data.numpy())
state2, reward, done, info = env.step(action)
동작을 실행하면 환경은 새 상태 s_2와 보상 r_2를 돌려준다. 에피소드가 끝난 후 정책망을 갱신할 때 이들을 사용하려면 이들을 적절한 배열에 추가해 두어야 할 것이다.
이런 식으로 새 상태를 얻어서 다시 모형을 실행하고 동작을 선택하는 과정을 에피소드가 끝날 때까지 반복한다.
모델의 훈련
모델의 훈련은 다음 세 단계로 이루어진다.
- 각 시간 단계에서 취한 동작의 확률을 계산한다.
- 그 확률에 할인된 총 수익(보상들의 합)을 곱한다.
- 확률 가중 총 수익(확률이 곱해진 수익)으로 역전파를 실행해서 손실값이 최소가 되도록 매개변수들을 갱신한다.
그럼 각 단계를 차례로 살펴보자.
동작 확률 계산
동작 확률의 경우, 신경망의 출력층에 존재하는 Softmax 함수에 의해 구해진다.
향후 보상의 계산
CartPole은 마지막 동작보다 첫 동작이 더 중요하다.
CartPole은 승리가 없고, 막대가 넘어지면 패배로 간주된다.
따라서 마지막 동작은 게임의 패배로 직접 이어지지만 첫 동작은 게임 패배의 주된 원인으로 보기 어렵다고 보자.
따라서 다음과 같이 지수적으로 감소하는 할인율을 적용하자.
gamma_t = [0.99,0.99,0.99,0.99,0.99]
exp = [1,2,3,4,5]
torch.power(gamma_t, exp)손실함수
할인된 보상들을 구한 후에는 그것들로 손실을 계산해서 정책망을 훈련한다.
앞에서 논의했듯이 손실은 아래 수식으로 표현된다.

이를 코드로 나타내보자.
def discount_rewards(rewards, gamma = 0.99):
lenr = len(rewards)
disc_return = torch.pow(gamma, torch.arange(lenr).float()) * rewards # 지수적으로 감소하는 보상 계산
disc_return /= disc_return.max() # [0,1]구간 정규화
return disc_return마지막에 정규화를 통해 학습의 안정성을 높이는 작업을 진행했다.
역전파
이제 손실 함수를 정의하고, 역전파해서 매개변수를 갱신하는 작업을 수행해보자.
위에서 정의한대로 손실함수는 다음과 같이 구현 가능하다.
def loss_fn(preds, r):
return -1 * torch.sum(r*torch.log(preds))전체 훈련 루프
전체 훈련 루프는 아래와 같다.
import gymnasium as gym
import numpy as np
import torch
import matplotlib.pyplot as plt
l1 = 4
l2 = 150
l3 = 2
model = torch.nn.Sequential(
torch.nn.Linear(l1, l2),
torch.nn.LeakyReLU(),
torch.nn.Linear(l2, l3),
torch.nn.Softmax(dim=0),
)
learning_rate = 0.009
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
env = gym.make('CartPole-v1', render_mode='human')
def discount_rewards(rewards, gamma = 0.99):
lenr = len(rewards)
disc_return = torch.pow(gamma, torch.arange(lenr).float()) * rewards # 지수적으로 감소하는 보상 계산
disc_return /= disc_return.max() # [0,1]구간 정규화
return disc_return
def loss_fn(preds, r):
return -1 * torch.sum(r*torch.log(preds))
MAX_DUR = 200
MAX_EPISODES = 500
gamma = 0.99
score = []
for episode in range(MAX_EPISODES):
curr_state = env.reset()[0]
done = False
transitions = []
for t in range(MAX_DUR):
act_prob = model(torch.from_numpy(curr_state).float())
action = np.random.choice(np.array([0, 1]), p=act_prob.data.numpy())
prev_state = curr_state
curr_state, _, terminated, truncated, info = env.step(action)
transitions.append((prev_state, action, t+1))
done = terminated or truncated
if done:
break
ep_len = len(transitions)
score.append(ep_len)
reward_batch = torch.Tensor([r for (s, a, r) in transitions]).flip(dims=(0, ))
disc_rewards = discount_rewards(reward_batch)
state_batch = torch.Tensor([s for (s, a, r) in transitions])
action_batch = torch.Tensor([a for (s, a, r) in transitions])
pred_batch = model(state_batch)
prob_batch = pred_batch.gather(dim=1, index=action_batch.long().view(-1, 1)).squeeze()
loss = loss_fn(prob_batch, disc_rewards)
optimizer.zero_grad()
loss.backward()
optimizer.step()
def running_mean(x, N=50):
kernel = np.ones(N)
conv_len = x.shape[0]-N
y = np.zeros(conv_len)
for i in range(conv_len):
y[i] = kernel @ x[i:i+N]
y[i] /= N
return y
score = np.array(score)
avg_score = running_mean(score, 50)
plt.figure(figsize=(10,7))
plt.ylabel("Episode Duration",fontsize=22)
plt.xlabel("Training Epochs",fontsize=22)
plt.plot(avg_score, color='green')
plt.show()
이번 장의 결론
REINFORCE는 정책 함수를 효과적이고 아주 손쉽게 훈련하는 한 방법이다.
그러나 너무 단순한 감이 있다.
CartPole처럼 상태 공간이 아주 작고 동작의 수도 아주 적은 간단한 게임에서는 REINFORCE가 잘 작동한다.
그러나 가능한 동작이 훨씬 많으면, 각 에피소드에서 그 동작들을 모두 강화했을 때 평균적으로 좋은 동작만 강화되리라고 기대하기가 어렵다.
좀 더 다양하고 정교한 에이전트를 훈련하는 방법들을 배워야 할 때다.
이번 장에서 배운 것
- 확률은 어떤 불확실한 과정이 산출하는 서로 다른 결과들에 대한 확신도(우도)를 배정하는 수단이다.
- 확률분포는 가능한 결과들에 배정한 확률들 전체를 특징짓는 수단이다.
하나의 확률분포는 P:O->[0,1], 즉 가능한 모든 결과를 [0, 1]구간의 실수로 사상하는 함수로 간주할 수 있다.
이때 모든 결과에 관한 이 함수의 합은 반드시 1이어야 한다. - 퇴화 분포(degenerate probability distribution)는 특정한 결과 하나만 추출되는(즉, 그 결과만 확률이 1이고 나머지 모든 결과의 확률은 0인)확률분포이다.
- 확률분포의 모드(mode)는 그냥 '봉우리', 즉 확률분포를 그래프로 그렸을 때 불쑥 솟은 부분의 또다른 이름이다.
- 조건부 확률은 어떤 추가적인 정보가 주어졌을 때의 결과의 확률, 즉 다른 어떤 사건을 조건으로 하는 확률이다.
- 정책은 상태를 동작으로 사상하는 함수 π:S->A이다. 정책은 일반적으로 주어진 상태에서 가능한 모든 동작에 대한 확률분포를 산출하는 확률적 정책 함수 π:P(A|S)의 형태로 구현된다.
- 수익은 하나의 에피소드 전체에 대해 환경이 제공한 보상들을 적절히 할인해서 합한 값이다.
- 정책 기울기 방법은 강화학습 접근 방식의 하나로, 매개변수화된 함수를 정책 함수로 사용해서 정책을 직접 배우려 한다.
흔히 신경망을 정책 함수로 두고, 관측된 보상들에 기초해서 동작 확률들이 개선되도록 신경망을 훈련한다. - REINFORCE 알고리즘은 정책 기울기 방법의 가장 간단한 예이다.
본질적으로 이 알고리즘은 (주어진 상태에서) 각 동작의 확률에 그 동작에 대한 보상을 곱한 값을 최대화하기 위해 동작의 확률을 보상의 크기에 비례해서 조정한다.
'AI Repository > 기초 강화학습' 카테고리의 다른 글
| [강화학습] A2C (0) | 2025.09.21 |
|---|---|
| [강화학습] Target Network를 이용한 안정성 개선 (0) | 2025.09.12 |
| [강화학습] Experience Replay, ER - Catastrophic Forgetting의 해소 (0) | 2025.09.12 |
| [강화학습] DQN (0) | 2025.09.12 |
| [강화학습] 강화학습에 신경망 더하기 (0) | 2025.09.01 |