[USACO Silver] 1차원 누적 합

PS/USACO Silver

조금씩 차근차근 2025. 9. 6. 14:55

아래 내용은 미국 정보 올림피아드인 USACO의 알고리즘 문제 학습 가이드인 usaco.guide를 참고하여 작성되었습니다

Introduction to Prefix Sums

Computing range sum queries in constant time over a fixed 1D array.

usaco.guide

시작 전에 이 문제를 풀어보고 오자.
난이도: Very Easy

Library Checker

judge.yosupo.jp

길이가 N인 다음 값을 계산하기 원하는 1차원 정수 배열이 있다고 가정해보자.

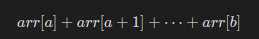
우리는 여기서 서로 다른 Q개의 쿼리를 (a,b)으로 보낼 것이다.
그때의 (a, b)는아래 식을 만족한다.

간단한 예시를 위해, N을 6으로 두고 문제를 풀어보자.

인덱스 i	1	2	3	4	5	6
arr[i]	1	6	4	2	5	3

무식하게는, 각 쿼리에 대하여 a부터 b까지 순회하며 합을 구할 수 있을것이다.

쿼리가 Q개가 있고, 각 쿼리를 계산하는 데 최대 O(N) 연산이 필요하므로 전체 시간복잡도는 O(QN)이 될 것이다.
이런 2차 수준의 시간복잡도는 아쉬움이 있으며, 더욱 더 최적화할 전략 또한 존재한다.

여기서 우리는 누적 합 개념을 도입할 수 있다.
접두사 합 배열을 prefix[] 라고 정의해보자.

여기서 먼저 배열을 1-indexed로 생각할 것이기 때문에, prefix[0] = 0으로 해당 prefix 배열을 다음과 같이 정의한다.

여기서 우리는 수학적 귀납법을 통해 점화식을 정의할 수 있다.

이 코드의 계산 과정은 O(N)이 될 것이다.

k는 N보다 작거나 같을 것이기 때문이다.

인덱스 i	0	1	2	3	4	5	6
prefix[ i ]	0	1	7	11	13	18	21

이제 우리가 [a, b] 구간의 합을 구한다고 하면, 다음과 같은 공식을 사용 가능하다.

이를 Prefix Sum 배열로 나타내면 아래와 같이 간다.

이제 우리는 [a, b] 구간에 대한 구간합을 구할 때, 단순히 해당 배열을 두번만 참조해서 O(1)에 수행할 수 있게 되었다.
즉, Q개의 각 쿼리마다 O(1)의 시간을 사용하므로, 시간복잡도는 O(N+Q)가 된다.

간단한 예시로 위에 선언한 배열의 [2,5] 구간의 합을 구해보자.

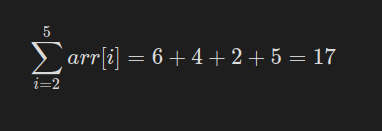
인덱스 i	1	2	3	4	5	6
arr [ i ]	1	6	4	2	5	3

이를 prefix sum을 이용하면 이렇게 구할 수 있다.

인덱스 i	0	1	2	3	4	5	6
prefix[ i ]	0	1	7	11	13	18	21

위 문제의 소스코드

Go Gradually - Repository