[USACO Gold] Knapsack DP - 배낭 문제를 다이나믹 프로그래밍으로 풀기

PS/USACO Gold

[USACO Gold] Knapsack DP - 배낭 문제를 다이나믹 프로그래밍으로 풀기

조금씩 차근차근 2025. 9. 11. 21:07

배낭(knapsack) 문제는 보통 제한된 용량의 컨테이너에 물건들의 부분집합을 넣되, 물건과 관련된 어떤 양을 세거나(카운트) 최적화하는 문제를 다룬다.
거의 항상 각 물건은 양의 무게를 가지며, 우리가 선택한 물건들의 총 무게는 어떤 수로 주어지는 컨테이너의 용량을 초과해서는 안 된다.

배낭 유형 문제의 변형으로는 다음과 같은 것들이 있다.

0/1 배낭 문제: 물건들의 부분집합을 골라 총 가치를 최대화하되, 총 무게가 컨테이너의 용량을 넘지 않도록 한다.
가능한 총 무게 찾기: 컨테이너 용량을 넘지 않게 임의의 부분집합으로 만들 수 있는 모든 총 무게를 구한다.
정확히 채우는 경우의 수 세기: 총 무게가 정확히 컨테이너 용량이 되도록 하는 물건의 순서열이 몇 개인지 센다(순서가 중요할 수도 있고 중요하지 않을 수도 있다).

배낭 문제의 동적 계획법(DP) 해법은 보통 상태(state)에 배낭의 남은 용량을 포함하고, 전이는 어떤 물건을 배낭에 추가해 보는 식으로 이뤄진다.

경쟁 프로그래밍에서는 고전적인 배낭 문제가 다양한 트릭, 위장, 추가 상태 정보와 함께 출제될 수 있다.

문제 - Dice Combinations

https://cses.fi/problemset/task/1633

CSES - Dice Combinations

CSES - Dice Combinations Time limit: 1.00 s Memory limit: 512 MB Your task is to count the number of ways to construct sum n by throwing a dice one or more times. Each throw produces an outcome between 1 and 6. For example, if n=3, there are 4 ways: Input

cses.fi

아래로 진행하기 전에, 꼭 한번 (10분이라도 직접) 생각해보자!

해법 – Dice Combinations(주사위 조합)

시간 복잡도: O(N)

문제는 주사위를 굴렸을 때 윗면의 합이 N이 되도록 하는 순서열이 몇 개인지를 묻는다(N <= 10^6).
배낭 비유를 유지하자면, 무게가 1부터 6까지인 물건이 무한히 많고, 어떤 순서로 물건을 컨테이너에 넣었을 때 컨테이너가 정확히 꽉 차는(합이 정확히 N이 되는) 순서열의 개수를 세려는 것이다.
이 문제에서는 물건(주사위 눈)의 순서가 중요하다.

편의를 위해, dp[x]를 합이 x가 되도록 하는 주사위 굴림 순서열의 개수로 두자.
우리가 구하고 싶은 것은 dp[N]이며, 이를 위해 합을 N으로 만드는 마지막 주사위 눈을 살펴보자.

마지막 눈이 1이라면, 마지막 눈이 1인 경우의 수는 dp[N-1]개이다.
마지막 눈이 2라면 dp[N-2]개, 이런 식으로 6까지 모두 고려하면 다음을 얻게 된다.

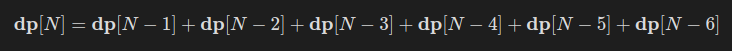
이를 x에 대해 일반화하면,

초기 조건으로 dp[0] = 1에서 시작하고, 이 점화식을 이용해 dp[1], dp[2], dp[3], …을 순차적으로 계산해 dp[N]을 구할 수 있다.
코드에서는 x < 0인 경우의 dp[x]는 무시한다는 점에 유의하자.

push dp 구현

import java.io.*;  

public class DiceCombinations {  
    public static void main(String[] args) throws IOException {  
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));  
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));  

        long n = Long.parseLong(br.readLine());  

        long[] dp = new long[(int) n + 1];  
        dp[0] = 1;  
        long mod = 1000000007L;  
        for (int i = 0; i < n; i++) {  
            for (int dice = 1; dice <= 6; dice++) {  
                if (i + dice <= n) {  
                    dp[i + dice] += dp[i];  
                    dp[i + dice] %= mod;  
                }  
            }  
        }  
        pw.println(dp[(int) n]);  
        br.close();  
        pw.close();  
    }  
}

pull dp 구현

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n;
        n = Integer.parseInt(br.readLine());

        long dp[] = new long[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= 6; j++) {
                if (i - j >= 0) { dp[i] += dp[i - j]; }
            }
            dp[i] %= 1000000007;
        }

        System.out.println(dp[n]);
    }
}