MountainCar - Policy Gradient Methods, 그리고 회귀

다양한 알고리즘의 고민

이전 글에서 이것 저것 수행해보고 난 뒤, 좀 더 다양한 기법들에 대해 트레이드오프를 이해할 필요성을 느낀 나는 다양한 알고리즘을 공부했다.

 

하지만 이번 MountainCar 환경에서는, 결국 DQN으로 다시 회귀할 수밖에 없었다.
그 근거는 다음과 같다.

• 나는 최근 다양한 정책 경사 알고리즘들을 공부해왔는데, 각 알고리즘은 해결하고자 하는 문제가 현재 MountainCar 의 상황과 맞지 않았다.
• 하이퍼파라미터 튜닝은 예술의 영역이고, 숙련자들 또한 기존에 푼 문제와 논문에 존재하는 하이퍼파라미터를 참고하여 하이퍼파라미터를 설정한다는 것을 확인했다.

 

---

REINFORCE

REINFORCE는 가장 기초적인 Policy Gradient Method로, 다음과 같은 이점과 한계를 갖고 있다.

이점

• 정책 자체를 신경망을 통해 결정하기 때문에, 입실론-그리디 정책과 같은 다소 "덜 구조적"인 방식에 비해 환경에 맞춰 체계적으로 정책을 선택할 수 있다.

한계

• 반드시 에피소드가 끝나야만 학습(정책의 변화)가 생기기 때문에, MountainCar와 같은 보상이 희소한 환경(산을 올라야 하는데, 이전에 "잘 행동"해두지 않으면 산을 오르기 어렵다)에서는 학습이 매우 불리하다.
• Policy Gradient Methods의 경우, 신경망으로 다음에 수행할 정책을 결정하기 때문에 오는 "연속적인 정책 결정"에서의 표현력 강화라는 이점이 있는데, 현재 MountainCar는 다소 이산적인 정책 공간으로, Policy Gradient Methods가 갖는 이점이 거의 없다.

A2C

A2C는 대표적인 온-폴리시 방식으로, 현재 문제에 맞지 않았다.

• 먼저, 단순한 액터-크리틱은 정책 기반 방법과 가치 기반 방법의 장점을 결합한 것이다.
  • 정책 기반 기법의 좋은/나쁜 행동을 구분할 수 없는 문제를 비평자의 행동 평가로 구분
  • 정책 기반 기법의 장점인 연속적인 행동 공간에서 잘 작동
  • 정책 기반 기법의 쉽게 발산하고 수렴성이 낮은 문제를 비평자를 통해 해결
  • 가치 기반 기법의 높은 수렴성을 취함.
  • 가치 기반 기법의 탐색 전략에 대한 하이퍼파라미터 민감성을 정책 신경망을 통해 해결
• A2C(Advantage Actor-Critic)은 단순 액터-크리틱의 고분산 문제를 해결하기 위해 등장했다.
  • 단순 액터 크리틱에서는 그 시점 이후의 모든 보상인 수익 G를 바로 쓰기 때문에, 여전히 값의 분산이 매우 높다.
    • 그런데, 수익의 정확한 값이 필요한게 아니다.
    • 우리는 '다른 행동과 비교해서 이 행동이 얼마나 나은가?'만 판단하면 되는데, 수익의 정확한 값이 나오는 바람에 학습에 끼치는 영향이 강화되고 있다.
    • A2C는 이것을 간단한 액터-크리틱의 발산의 원인으로 보았다.
  • 따라서 Advantage 개념을 도입해, 값의 분산을 줄여 발산하지 않도록 제어했다.

• MountainCar는 실제 보상(성공 에피소드 도달)이 매우 희소한 환경이다.
  • 실제 첫 보상에 도달하기가 매우 어렵다.
  • 온 폴리시 특성 상, 그 과정에서도 학습하게 되는데, 그 과정이 그대로 학습의 지연이 된다.

오프 폴리시는 평가와 개선의 대상인 정책(목표 정책 π)과 데이터를 모으는 정책(행동 정책, μ)을 구분했다.
하지만 온-폴리시는 데이터를 모으는 정책과 실제 평과와 개선의 대상인 정책이 구분되어 있지 않아, 매번 환경에서 직접 데이터를 받아와야 한다.
이는 환경을 구동하는 비용이 높은 경우(복잡한 시뮬레이션 환경, 현실 세계의 로봇 제어) 큰 오버헤드로 다가오게 된다.

PPO

PPO는 정책 학습시 KL Divergence의 급등을 정책 클리핑으로 제어하여 학습이 차근차근 진행되도록 만드는 알고리즘이다.

[정보 이론] KL Divergence (KL 발산) - 크로스 엔트로피를 쓰는 이유

 

• 정책 업데이트 시 기존 정책에서 크게 달라지는 걸(발산) 막기 위해 CPI(보수적 정책 iteration)라는 기법을 사용한다.
  • CPI는 성능이 하락하지 않도록 정책을 보수적으로 섞어 업데이트하면서, 성능의 하한을 보장하는 기능을 수행한다.
  • 그런데, CPI를 사용하더라도 iteration되면 정책이 크게 달라질 수 있다.
• PPO는 여기서 정책이 크게 달라지지 않도록, 달라지는 범위 자체를 클리핑으로 제한한다.
  • 즉, PPO의 클리핑은 큰 업데이트를 안정화할 뿐, 탐색/신호 부족을 해결해주진 않는다.
• 그리고 MountainCar는 실제 보상(성공 에피소드 도달)이 매우 희소한 환경이다.
  • 실제 첫 보상에 도달하기가 매우 어렵다.
  • 온 폴리시 특성 상, 그 과정에서도 학습하게 되는데, 그 과정이 그대로 학습의 지연이 된다.

단순 Q-Learrning

단순한 Q-Learning의 경우, 수학적으로 이론도 탄탄하고, 이산적인 공간에 유리하다.
하지만 연속적인 공간에 불리하다.

• argmaxₐ Q(s,a)가 비실용적이다.(메모리 효율이 나쁨)
  • 따라서 DDPG/TD3/SAC 같은 신경망 actor-critic로 우회하거나,
  • 또는 근사(이산화)로 극복한다.

현재 이걸 하고 있는 이유 - 일정 추천 기능 만들기

• 일정은 비교적 "연속적인 구간"에 배치될 수 있다.
  • 따라서 단순한 이산적인 형태의 선택지를 다루는 Q-Learning보단, 보다 연속적인 구간을 다룰 수 있는 정책망 계열에 익숙해져야 한다.
• 일정은 단순히 "남는 곳에 배치"하는 문제가 아니다.
  • 일정은 사용자의 일정 패턴을 고려한 위치에 배치하는 것이 핵심이다.
  • 따라서 이전의 상태에 영향을 받는다.
  • 단순 MDP보단, POMDP에 더욱 적절한 신경망 모델을 공부해야 한다.
• RLHF까지 가기 위해선, 신경망 훈련에 익숙해져야 한다.
  • 신경망 훈련에서 발생하는 문제와, 각 최적화 기법의 원리에 대해 이해하고 있어야 한다.
• 하지만, 이 문제에 정책망 도입은 과하다.
  • 선택할 수 있는 정책이 좌/멈춤/우 세 종류밖에 없다.
  • 연속적인 정책에서 고를거였으면, Mountain Car Continuous 문제를 풀었어야 했다.

따라서, DQN으로 풀기로 결정했다.

하이퍼파라미터 설정

우선, 논리적으로 살펴봤을 때 "잘 알려진" 하이퍼파라미터만 있다면 DQN도 이 문제를 잘 풀 수 있어야 함이 분명했다.
따라서 유명한 하이퍼파라미터 값을 탐색했다.

https://huggingface.co/sb3/dqn-MountainCar-v0

sb3/dqn-MountainCar-v0 · Hugging Face

이는 유명한 강화학습 알고리즘 라이브러리인 Stable Baseline3 의 MountainCar 예제이다.

해당 하이퍼파라미터를 참고하였는데, 인상적인 부분은 batch_size와 buffer_size였다.

나의 하이퍼파라미터는 1000, 32에 불과했는데, 이 설정은 각각 10000, 128로 잡아 희소한 보상이 빠르게 소실되는 문제를 해결한 점이 인상적이었다.

 

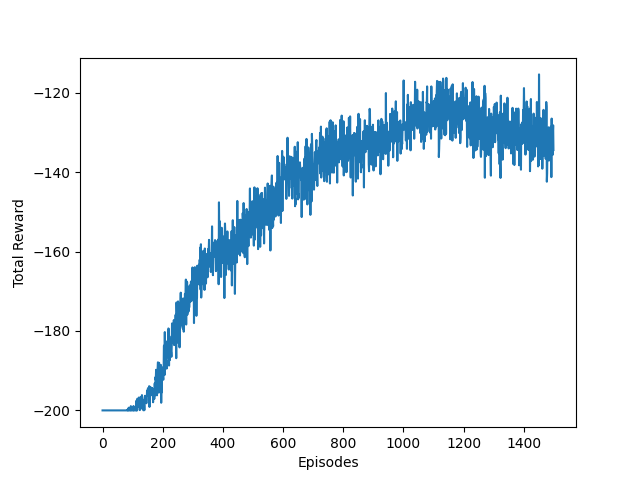
이를 통해 기존 보상이 -160에서 -120까지 올라간 것을 확인할 수 있다.

소스코드
agent.py

import random  
from collections import defaultdict, deque  

import numpy as np  
import torch  
import torch.nn as nn  


class QNet(nn.Module):  
    def __init__(self, action_size):  
        super().__init__()  
        self.action_size = action_size  
        self.l1 = nn.Linear(2, 256)  
        self.l2 = nn.Linear(256, 256)  
        self.l3 = nn.Linear(256, action_size)  

    def forward(self, x):  
        if x.dim() == 1:  
            x = x.unsqueeze(0)  
        x = torch.relu(self.l1(x))  
        x = torch.relu(self.l2(x))  
        x = self.l3(x)  
        return x  


class DQNAgent:  
    def __init__(self):  
        self.gamma = 0.99  
        self.lr = 0.004  
        self.buffer_size = 10000  
        self.batch_size = 128  
        self.action_space = 3  
        self.n_timesteps = 120_000  


        self.train_freq = 16              # every 16 env steps, do...  
        self.gradient_steps = 8           # ...8 optimization steps  

        self.eps_start = 1.0  
        self.eps_final = 0.07  
        self.exploration_fraction = 0.2  
        self.exploration_steps = int(self.n_timesteps * self.exploration_fraction)  

        self.global_step = 0  

        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")  
        print(f"Using device: {self.device}")  
        self.replay_buffer = ReplayBuffer(self.buffer_size, self.batch_size)  
        self.qnet = QNet(self.action_space).to(self.device)  
        self.target_qnet = QNet(self.action_space).to(self.device)  
        self.sync_qnet()  
        self.optimizer = torch.optim.Adam(self.qnet.parameters(), lr=self.lr)  
        self.loss_fn = nn.SmoothL1Loss()  

        # target sync  
        self.target_sync_every = 600  # steps  

    def epsilon(self):  
        if self.global_step >= self.exploration_steps:  
            return self.eps_final  
        # linear decay  
        frac = self.global_step / max(1, self.exploration_steps)  
        return self.eps_start + (self.eps_final - self.eps_start) * frac  

    def preprocess(self, s):  
        # 간단 스케일링  
        return np.array([s[0] / 0.6, s[1] / 0.07], dtype=np.float32)  


    def sync_qnet(self):  
        self.target_qnet.load_state_dict(self.qnet.state_dict())  

    def get_action(self, state):  
        if np.random.rand() < self.epsilon():  
            return np.random.choice(self.action_space)  
        with torch.no_grad():  
            s = torch.as_tensor(state, dtype=torch.float32, device=self.device).unsqueeze(0)  
            q_values = self.qnet(s)  
            return int(torch.argmax(q_values, dim=1).item())  

    def update(self, state, action, reward, next_state, done):  
        self.global_step += 1  
        self.replay_buffer.add(state, action, reward, next_state, done)  
        if len(self.replay_buffer) < 1000:  
            return  

        if self.global_step % self.train_freq != 0:  
            return  

        for _ in range(self.gradient_steps):  
            state, action, reward, next_state, done = self.replay_buffer.get_batch()  

            s  = torch.as_tensor(state,      dtype=torch.float32, device=self.device)  
            a  = torch.as_tensor(action,     dtype=torch.int64,   device=self.device)  
            r  = torch.as_tensor(reward,     dtype=torch.float32, device=self.device)  
            ns = torch.as_tensor(next_state, dtype=torch.float32, device=self.device)  
            d  = torch.as_tensor(done,       dtype=torch.float32, device=self.device)  


            qs = self.qnet(s).gather(1, a.unsqueeze(1)).squeeze(1)  

            with torch.no_grad():  
                next_qs = self.target_qnet(ns)  
                next_q = next_qs.max(dim=1)[0]  
                target = r + (1 - d) * self.gamma * next_q  


            self.qnet.zero_grad(set_to_none=True)  
            loss = nn.MSELoss()(qs, target)  
            loss.backward()  
            self.optimizer.step()  

        # step 기준 타깃 동기화  
        if self.global_step % self.target_sync_every == 0:  
            self.sync_qnet()  


class ReplayBuffer:  
    def __init__(self, buffer_size, batch_size):  
        self.buffer = deque(maxlen=buffer_size)  
        self.batch_size = batch_size  

    def add(self, state, action, reward, next_state, done):  
        self.buffer.append((state, action, reward, next_state, done))  

    def get_batch(self):  
        samples = random.sample(self.buffer, self.batch_size)  

        state = np.stack([x[0] for x in samples])  
        action = np.array([x[1] for x in samples])  
        reward = np.array([x[2] for x in samples])  
        next_state = np.stack([x[3] for x in samples])  
        done = np.array([x[4] for x in samples]).astype(np.int32)  
        return state, action, reward, next_state, done  

    def __len__(self):  
        return len(self.buffer)

train.py

import gymnasium as gym  
import matplotlib.pyplot as plt  
from agent import DQNAgent  
import time  

start = time.time()  

episodes = 1500  
sync_interval = 20  
env = gym.make("MountainCar-v0", render_mode="rgb_array")  
reward_histories = []  
for trial in range(40):  
    agent = DQNAgent()  
    reward_history = []  
    for episode in range(episodes):  
        state = env.reset()[0]  
        done = False  
        total_reward = 0  

        while not done:  
            action = agent.get_action(state)  
            next_state, reward, terminated, truncated, _ = env.step(action)  
            origin_reward = reward  
            done = terminated | truncated  

            agent.update(state, action, reward, next_state, done)  
            state = next_state  
            total_reward += origin_reward  
        reward_history.append(total_reward)  
    reward_histories.append(reward_history)  
    print(trial)  


end = time.time()  

print(f"실행 시간: {end - start:.4f}초")  

reward_means = [sum(col)/len(col) for col in zip(*reward_histories)]  

plt.plot(reward_means)  
plt.xlabel('Episodes')  
plt.ylabel('Total Reward')  
plt.show()

신경망으로 푸는 해는 주로 Double DQN이라고 하니, 이 부분또한 추가로 학습해봐야 겠다.