[USACO Gold] Divisibility - PS(알고리즘)에서의 나눗셈
이와 같은 수학 문제는 코딩 테스트에는 잘 출제되지 않기 때문에 건너뛰는 사람들도 많지만,
나는 시간복잡도 계산에 가장 강력한 인사이트를 부는 내용이 바로 이 수학 부분이라고 생각한다.
그래서 이 수학 파트도 건너뛰지 않고 어느정도 설명을 진행하도록 하겠다.
소인수분해 (Prime Factorization)
양의 정수 a가 음이 아닌 정수 b의 약수(divisor) 또는 인수(factor)라고 불리는 것은, b가 a로 나누어떨어진다는 의미이다. 즉, 어떤 정수 k가 존재하여 b = ka가 되는 경우이다.
정수 n > 1이 소수(prime)라는 것은 그 약수가 1과 n뿐일 때를 말한다.
1보다 큰 정수 중 소수가 아닌 수는 합성수(composite)라고 한다.
모든 양의 정수는 유일한 소인수분해를 가진다. 즉, 소수들의 곱으로 분해할 수 있으며, 다음과 같이 표현된다.
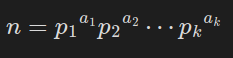
여기서 p_i는 서로 다른 소수이고, a_i는 양의 정수이다.
이제 임의의 양의 정수의 소인수분해를 찾는 방법을 살펴보자.
List<Integer> factor(int n) {
List<Integer> factors = new ArrayList<>();
for (int i = 2; i * i <= n; i++) {
while (n % i == 0){
factors.add(i);
n /= i;
}
}
if (n > 1) factors.add(n);
return factors;
}이 알고리즘은 O(sqrt{n}) 시간에 동작한다. 그 이유는 for 루프가 최대 루트 n번의 나눗셈 검사를 수행하기 때문이다.
내부에 while 루프가 있긴 하지만, n을 i로 나누면서 n의 크기가 빠르게 줄어들기 때문에 실제로는 반복 횟수가 줄어들어 속도가 향상된다.
예시로 n = 252일 때 알고리즘이 어떻게 동작하는지 보자.
| i | n | ret |
|---|---|---|
| 2 | 252 | {} |
| 2 | 126 | {2} |
| 2 | 63 | {2, 2} |
| 3 | 21 | {2, 2, 3} |
| 3 | 7 | {2, 2, 3, 3} |
이 시점에서 for 루프는 종료된다. 왜냐하면 i가 이미 3이고, 이는 7^1/2 보다 크기 때문이다.
마지막 단계에서 7을 인수 목록 v에 추가해야 한다. (그러지 않으면 7이 포함되지 않는다.)
따라서 최종 소인수분해 결과는 ${2, 2, 3, 3, 7}$이 된다.
약수 세기 (Counting Divisors)
CSES - Easy
https://cses.fi/problemset/task/1713
CSES - Counting Divisors
CSES - Counting Divisors Time limit: 1.00 s Memory limit: 512 MB Given n integers, your task is to report for each integer the number of its divisors. For example, if x=18, the correct answer is 6 because its divisors are 1,2,3,6,9,18. Input The first inpu
cses.fi
해법 – 약수 세기
가장 직관적인 방법은 문제에서 요구하는 그대로 구현하는 것이다. 즉, 각 x에 대해 O(sqrt x) 시간에 약수의 개수를 구하는 것이다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
PrintWriter pw = new PrintWriter(new BufferedOutputStream(System.out));
int T = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while (T-- > 0) {
sb.append(solve(br)).append("\n");
}
pw.print(sb);
br.close();
pw.close();
}
public static int solve(BufferedReader br) throws IOException {
int x = Integer.parseInt(br.readLine());
int count = 0;
for (int i = 1; i * i <= x; i++) {
if (x % i == 0) {
count++;
if (x / i != i) count++;
}
}
return count;
}
}이 방법은 O(n x^1/2) 시간에 실행된다.
이는 정답을 받기에는 충분히 빠르지만, 사실 더 최적화하여 O((x + n) log x) 시간에 해결할 수 있다!
먼저 소인수분해의 중요한 성질을 보자.

이때 $x$의 약수 개수는

개 이다.
왜 그럴까?
x의 임의의 약수에서 p_i의 지수는 [0, a_i] 범위에 있어야 하며, 각 지수는 서로 다른 약수를 만들어낸다. 따라서 p_i는 a_i + 1개의 선택지를 제공하며, 곱하면 전체 약수 개수가 된다.
x는 O(log x) 개의 서로 다른 소인수를 가질 수 있다. 따라서 x의 소인수분해를 효율적으로 찾을 수 있다면, 위의 성질을 이용해 O(log x) 시간에 쿼리에 답할 수 있다.
소인수분해를 O(log x)에 구하기
- 각 k <= 10^6에 대해 k를 나누는 임의의 소수를 찾는다.
- 이를 찾기 위해 에라토스테네스의 체(Sieve of Eratosthenes)를 사용한다. 이 방법은 O(nlog n)에 동작한다.
- 체를 이용하면 x를 미리 계산한 소수로 나누어가며 x=1이 될 때까지 소인수분해할 수 있다.
import java.io.*;
import java.util.ArrayList;
import java.util.List;
public class Main {
public static List<Integer> primes = new ArrayList<>();
static int MAX = 1000000;
static int[] check = new int[MAX + 1];
public static void main(String[] args) throws Exception {
for (int i = 2; i <= MAX; i++) {
if (check[i] == 0) {
for (int j = i; j <= MAX; j += i) {
check[j] = i;
}
}
}
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
int T = Integer.parseInt(br.readLine());
StringBuilder builder = new StringBuilder();
while(T-->0){
builder.append(solve(br, pw)).append('\n');
}
pw.print(builder);
br.close();
pw.close();
}
/**
* x의 약수 개수 구하기
* 6의 경우
* 1 2 3 6
* 2 * 2 * 8의 경우
* 2 2 2
* 4 * 10의 경우
* 2 5
* 9의 경우
* 3 3
* 16의 경우
* 2 2 2 2
*/ public static int solve(BufferedReader br, PrintWriter pw) throws IOException {
int x = Integer.parseInt(br.readLine());
int ans = 1;
while (x != 1) {
int count = 1;
int prime = check[x];
while (x % prime == 0) {
count++;
x /= prime;
}
ans *= count;
}
return ans;
}
}최대공약수 (GCD) & 최소공배수 (LCM)
GCD
두 정수 $a$와 $b$의 최대공약수(GCD)는 두 수를 나눌 수 있는 가장 큰 정수이다.
이를 구하기 위해 유클리드 호제법(Euclidean Algorithm)을 사용한다:

구현 예시:
public int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}이 알고리즘은 O(log ab)에 실행된다.
최악의 경우는 a, b가 연속된 피보나치 수일 때 발생한다. 예를 들어,

이 되어 총 n+1번의 호출이 필요하다. 이는 log(F_n F_{n+1})에 비례한다.
LCM
두 정수 a, b의 최소공배수(LCM)는 두 수 모두로 나누어지는 가장 작은 정수이다.
이는 다음 성질을 이용해 계산할 수 있다.
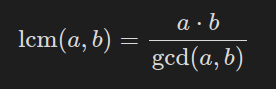
주의:
a * b / gcd(a, b)로 구현하면 a * b가 자료형 범위를 초과할 경우 정수 오버플로우가 발생할 수 있다.
따라서 먼저 a를 gcd(a, b)로 나눈 뒤 b를 곱하면 안전하다.
GCD와 LCM은 결합법칙을 만족하므로 여러 수의 GCD/LCM을 계산할 때 순서에 상관없이 2개씩 묶어서 계산하면 된다.
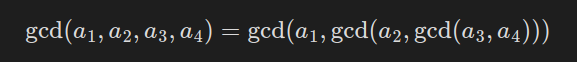
추천 문제
Easy
공식 해설이 없어, 핵심 아이디어와 정답 코드로 대체함.
- 각 수열 내 원소들이 이루는 사이클의 lcm이 정답.
- 나눗셈의 경우, 모듈러 연산으로 인한 합동이 잘 이루어지지 않음에 주의
- lcm을 구할 때, a*b/gcd(a, b) 가 아닌, 직접 인수 곱을 이용해야 안전함.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class PermutationRounds {
public static final int MAX_VAL = 200000;
static int[] prime = new int[200001];
public static void main(String[] args) throws IOException {
setPrime();
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] arr = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).map(a -> a - 1).toArray();
int[] check = new int[MAX_VAL + 1];
Arrays.fill(check, -1);
int[] lcm = new int[MAX_VAL + 1];
for(int i = 0; i < n; i++){
if(check[i] != -1) continue;
long count = 1;
check[i] = 1;
int now = arr[i];
check[now] = 1;
while (now != i){
now = arr[now];
check[now] = 1;
count++;
}
lcm(count, lcm);
}
long ans = getPow(lcm);
System.out.println(ans);
br.close();
}
private static long getPow(int[] lcm) {
long ans = 1;
for(int i = 1; i <= MAX_VAL; i++){
long now = i;
while(lcm[i] > 0){
if(lcm[i] % 2 == 1){
ans = (ans * now) % 1000000007L;
}
now *= now;
now %= 1000000007L;
lcm[i] >>= 1;
}
}
return ans;
}
private static void setPrime() {
for(int i = 2; i <= MAX_VAL; i++){
if(prime[i] == 0){
for(int j = i; j <= MAX_VAL; j += i){
prime[j] = i;
}
}
}
}
private static void lcm(long newVal, int[] lcm) {
while(newVal > 1){
int nowPrime = prime[(int)newVal];
int count = 0;
while(newVal % nowPrime == 0){
newVal /= nowPrime;
count++;
}
lcm[nowPrime] = Math.max(lcm[nowPrime], count);
}
}
static long modPow(long a, long e, long m) {
long r = 1 % m;
a %= m;
while (e > 0) {
if ((e & 1) == 1) r = (r * a) % m;
a = (a * a) % m;
e >>= 1;
}
return r;
}
static long invModPrime(long a, long m) {
return modPow(a, m - 2, m);
}
}
Normal
본 내용은 미국 정보 올림피아드인 USACO의 알고리즘 문제 학습 가이드인 usaco.guide를 참고하여 작성되었습니다.
Divisibility
Using the information that one integer evenly divides another.
usaco.guide
궁금한 문제가 있으시거나 해설에 이해가 되지 않는 부분이 있다면 댓글 달아주시면 풀어드립니다.
오일러 피-함수 내용의 경우, 제대로 설명하려면 페르마의 소정리 및 모듈러 역원 개념까지 함께 다루는게 좋을 것 같아 다루지 않았습니다.
참고하시길 바랍니다.