[9376] 탈옥
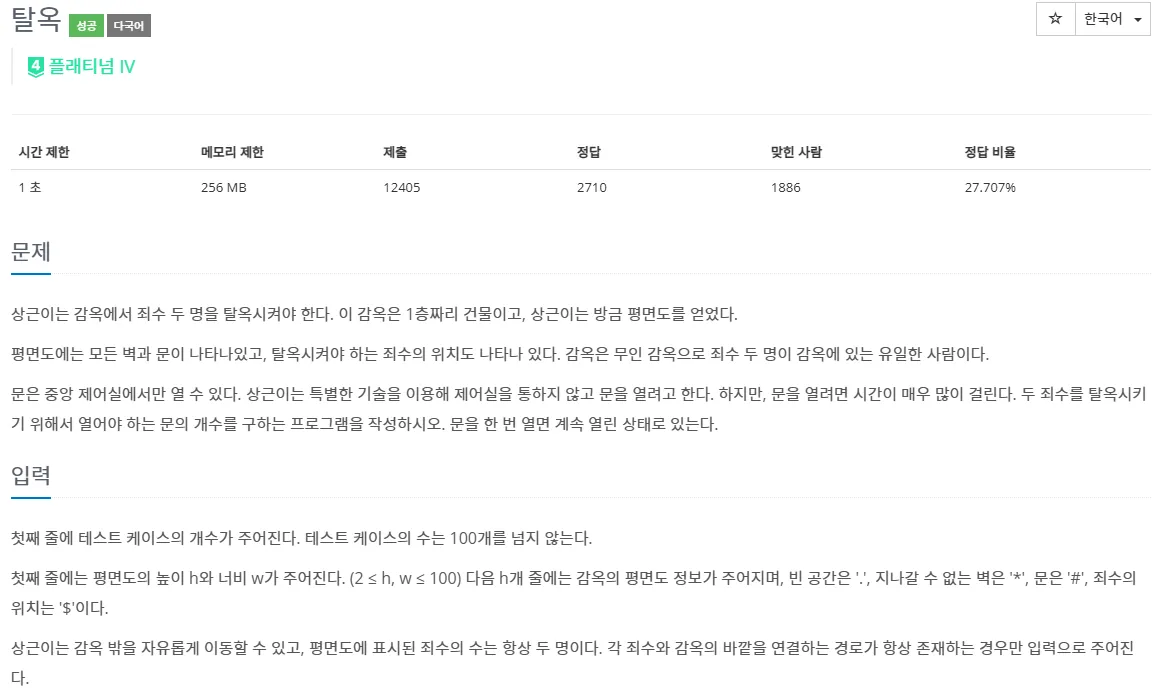
기본적인 0-1 BFS 문제처럼 보인다.
deque를 이용하면, push_front() 및 push_back() 을 이용해 열어야 하는 문의 갯수를 셀 수 있다.
근데 단순 최단거리가 아니다.
죄수 두명을 탈옥시켜야 한다.
탈옥의 정의는, 현재 보여지는 지도 밖으로 죄수가 나간다는 의미이다.
우리는 여기서, 지도 밖에 padding 을 한 줄 추가함으로서, 탈옥을 시킬 수 있다.
단순히 bfs 하면?
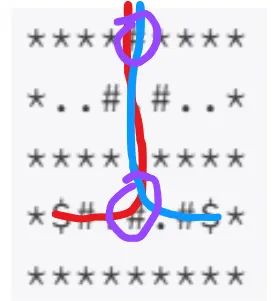
다음과 같이, 겹치는 지점을 제외해줘야 한다.
근데 두개의 거리를, 중복 없이 어떻게 잴 수 있지?
시나리오를 그려보며, 규칙성이 있는지 탐색해보면 반드시 어딘가에서 죄수 2명과 외부지점이 만날 수 있다.
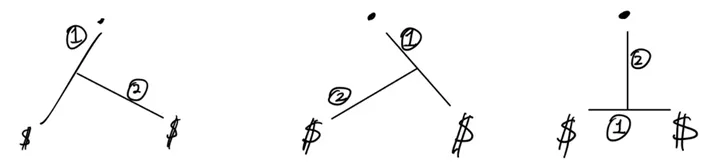
문제를 두번에 나눠서 풀면, 해를 구할 수 있지 않을까?

다음과 같은 경우, 두 죄수 사이의 최단 거리는 5이고, 이 최단 거리를 이용해서 밖까지의 최단거리를 구하면, 문제의 최적해인 9보다 높은 10이 나오게 된다.
어떻게 겹치는 거리 없이, 밖까지의 최단거리를 구할 수 있지?
이전에 죄수 A를 구하며 연 문 정보를 이용해, 죄수 B를 구하는 최단거리를 구하는 방법은 어렵다.
죄수 A를 구하며 얻은 최적해가, 죄수 B를 구하는데도 최적해라는 보장이 없다. 이는 외부 지점과 죄수를 넣어도 마찬가지이다.
한번에 둘을 깔끔하게 탈옥시킬 수 있는 방법이 필요하다.
문제 추가 분석
기존 분석 말고도, 예제 3에 나온 추가 케이스 하나가 더 있었다.
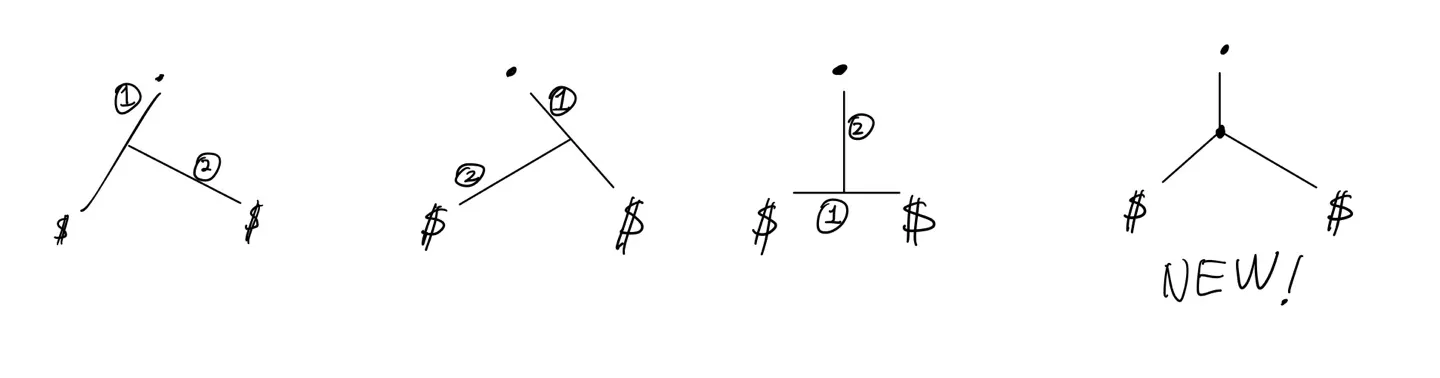
우리는 여기서 흥미로운 관찰을 수행할 수 있다.
반드시 세 지점이 만나는 “한 점”이 존재한다.
그 한 점은, 문에 걸리는 경우만 아니면, 거리가 중복계산될 경우가 없다.
증명
두 죄수는 “탈옥”되어야 한다.
만약 세 지점이 만나지 않으며, 두 죄수가 탈옥 가능한 경우가 있으려면, 감옥 밖이 자유롭게 이동이 불가능한 공간이어야 한다.
우리는 패딩을 더할 때, 감옥 밖은 문과 벽이 없는 단순 빈 공간으로 정의했다.
따라서 세 지점이 만나는 지점은 항상, 반드시 존재한다. 해당 지점을 A 라고 하자.
만약 A가 아닌 다른 지점에서 세 위치까지의 거리를 계산한다고 하면, 그 값은 반드시 A의 거리보다 크거나 같을 수밖에 없다.
구현
각 점 사이의 거리를 어떻게 구할 것인가?
- 모든 점 기준 세 점 사이의 거리를 구해야 하나?
- O(4hwhw) → 시간초과
- 죄수의 위치는 상수이다. 변하지 않는다.
- 우리는 여기서 각 점 사이의 거리는 미리 계산해놓을 수 있다는 것을 파악할 수 있다.
- 따라서, 먼저 각 세 점부터 다른 모든지점까지의 거리를 BFS로 계산하고, 각 점을 순회하며, 세 지점까지의 거리를 합산하여, 현재 지점부터 다른 세 점 까지의 거리를 계산한다.
예외 처리
- #에서 세 점 사이의 거리를 계산하면, 현재 #이 중복 계산된다.
- 따라서, 현재 지점이 # 일 경우, 세 거리의 합에 2를 빼야 한다.
- 방문 불가능한 공간이 있는 경우도 예외처리 해보자.
- 벽이거나
- 벽에 갇혀 도달할 수 없는 경우에는
- 세 지점이 만날 수 있는 지점이 아니므로, 값 계산에서 제외해야 한다.
