[밑바닥부터 시작하는 딥러닝] word2vec
본 내용은 밑바닥부터 시작하는 딥러닝 2도서를 참고하여 작성되었습니다.
밑바닥부터 시작하는 딥러닝 2 - 예스24
직접 구현하면서 배우는 본격 딥러닝 입문서 이번에는 순환 신경망과 자연어 처리다! 이 책은 『밑바닥부터 시작하는 딥러닝』에서 다루지 못했던 순환 신경망(RNN)을 자연어 처리와 시계열 데
www.yes24.com
앞 장에 이어서 이번 장의 주제도 단어의 분산 표현이다. (우리는 단어를 수치화된 벡터로 표현하고 싶었다.)
이번 장에서는 단순한 word2vec를 이용해, '추론 기반 기법'에 대해 알아보자.
참고로 이번 장에서 구현할 word2vec은 '단순한' word2vec이다.
이후 다음장에서 몇가지 개선을 통해 '진짜' word2vec을 구현할 것이다.
추론 기반 기법과 신경망
단어를 벡터로 표현하는 방법(분산 표현)은 지금까지 활발히 연구되었다.
그중에서도 성공적인 기법은 다음 두가지였다.
- 통계 기반 기법
- 추론 기반 기법
이번 절에서는 통계 기반 기법의 문제점을 지적하고, 그 대안인 추론 기반 기법의 이점을 거시적 관점에서 알아보자.
통계 기반 기법의 문제점
우리는 앞서 통계 기반 기법에 대해서 아래와 같은 작업을 수행했다.
- 전체 데이터셋에 대하여
- PPMI를 구하고
- SVD를 적용했다.
그런데 SVD는 O(n^3)의 시간복잡도를 갖는다.
만약 단어의 개수가 100만개라면, 10^21 의 시간이 필요하고, 일반적인 컴퓨터가 1초에 10^8개의 연산을 수행한다고 가정했을 때, 10^13초의 시간이 필요하다.
이는 컴퓨터가 슈퍼컴퓨터로 바뀌더라도 기다리기 힘든 시간이다.
또한, 통계 기반 기법은 전체 데이터셋에 대하여 1회 배치처리가 필요했다.
즉, 나눠서/이어서 학습이라는 개념이 존재하지 않고, 이는 새로운 단어의 도입에 까다로운 단점을 가지게 만들었다.

반면 추론 기반 기법은, 예컨데 신경망을 사용하는 경우에는 미니배치로 학습하는 것이 일반적이기에, 데이터가 많은 상황에서도 데이터를 나눠서 차근차근 작업할 수 있다.
또한, 여러 머신과 여러 GPU를 이용한 병렬 계산도 가능해져서 학습 속도를 높일 수도 있다.
이제 본격적으로 추론 기반 기법을 배워보자.
추론 기반 기법의 개요
추론 기반 기법은 우리가 수능 문제에서 자주 풀었던 "빈칸추론" 이다.

우리는 컴퓨터에게 빈칸을 주고 이 안을 채워보라고 이야기하고, 그 평가를 손실함수를 통해 수행할 것이다.
이번 장에선 쭉 이 예제를 가지고 word2vec을 학습할 것이다.
이러한 추론 문제를 반복해서 풀면서 단어의 출현 패턴을 학습하는 것이다.
이를 모델 관점에서 보면 아래 그림처럼 보이게 된다.

즉, 우리는 "어떠한 모델" 덕분에 각 단어의 출현 확률을 계산하는 방식으로 구현하게 된다.
그리고 그 학습 결과로 단어의 분산 표현을 획득(확률 분포)하는 것이 추론 기반 기법의 전체 그림이다.
신경망에서의 단어 처리
일단 신경망은 단어를 있는 그대로 처리할 수 없으니, 단어를 고정 길이의 벡터로 변환해야 한다.
이때 사용하는 대표적 방법이 "원-핫 인코딩"이다.
원-핫 인코딩이란, 벡터의 원소 중 하나만 1이고 나머지는 모두 0인 벡터화를 수행하는 것을 의미한다.
그 결과로 "원-핫 표현(원-핫 벡터)"를 얻게 된다.
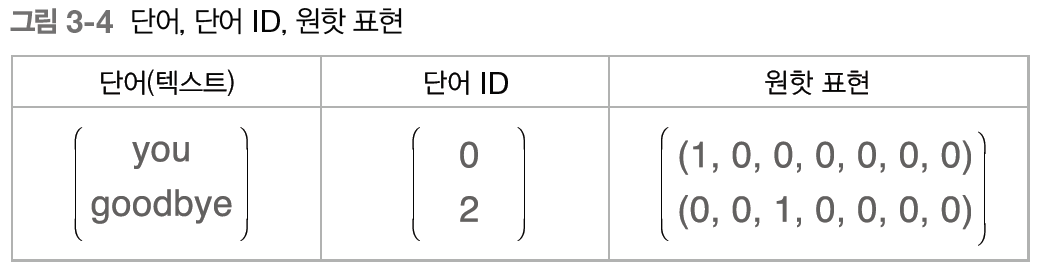
이를 위해선 어휘 수 만큼 원소를 갖는 벡터를 정의해야 한다.
입력 층 뉴런이 너무 많아지는 것 아닌가? 라는 의문이 생길 수 있는데, 추후 은닉층의 뉴런 수로 고정시킬 것이다. 일단은 입력층의 뉴런 수에 부담을 갖지 말자.
이렇게 입력층을 표현하면 아래와 같다.

이제 우리는 단어를 벡터로 나타낼 수 있게 되었다.
그리고 각 계층들은 벡터를 처리할 수 있다.
우리는 은닉층으로 3개의 뉴런을 준비했다.

은닉층의 뉴런은 해당 단어를 나타내는 고정된 크기의 벡터가 된다. 차차 따라가보자.
해당 은닉층은 완전 연결 계층으로, 가중치만 존재하고 편향이 존재하지 않는다.
즉, "행렬 곱"과 연산이 같아진다.
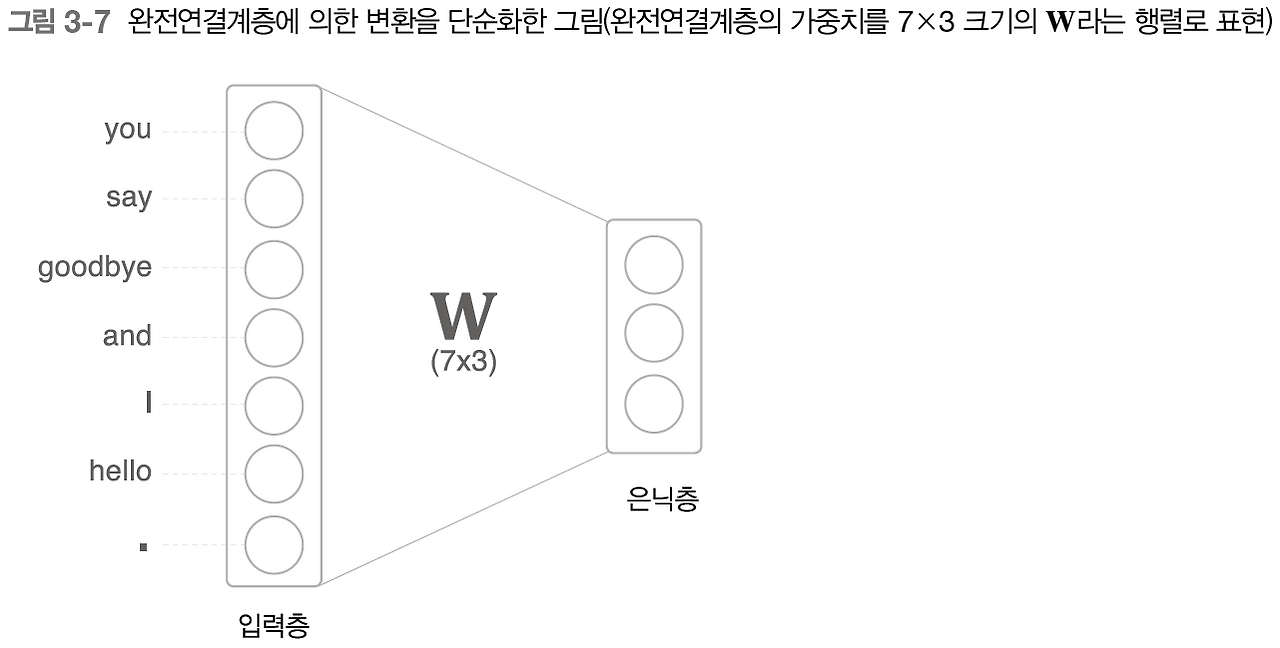
지금까지의 이야기를 코드로 표현해보자.

우리가 단어를 원-핫 인코딩한 형태를 다시 한번 생각해보자.
c는 하나의 1 외엔 전부 0이다.
cW는 결국 가중치의 행벡터 하나를 "뽑아낸" 것과 같아진다.

이 연산은 솔직히 비효율적이다. 굳이 행렬곱을 수행하긴 낭비다.
다음 장에서 이 개선을 알아볼 것이다.
그리고 아래와 같이, numpy 연산 대신, 행렬곱으로 해당 레이어를 대체하는 것도 가능하다.

이를 사용하면 다음과 같다.

단순한 word2vec
앞 절에서는 추론 기반 기법을 배우고, 신경망으로 단어를 처리하는 방법을 코드로 살펴봤다.
이제 드디어 word2vec 을 구현할 차례이다.
word2vec은 아래와 같은 종류가 있다.
- CBOW (n -> 1, 맥락 -> 타겟)
- skip-gram (1 -> n, 타겟->맥락)
우리는 이번 장에서 CBOW 중심으로 학습을 수행할 것이다.
skip-gram은 CBOW를 구현할 줄 알면 빠르게 학습/구현할 수 있으니 걱정하지 말자.
CBOW 모델의 추론 처리
CBOW는 위에서 언급했듯 맥락 -> 타깃 추측을 수행하는 신경망이다.
우리는 이 CBOW 모델이 가능한 한 정확하게 추론하도록 훈련시켜서 단어의 분산 표현을 획득할 것이다.
CBOW모델의 입력은 맥락이다.
맥락은 "you"와 "goodbye"와 같은 단어들의 목록으로, 여러개의 입력층이 존재한다.
이를 그림으로 표현하면 다음과 같다.

입력층이 2개 있고, 두 입력층에 전해진 값을 같은 완전연결계층(W_in)이 처리한다.
이후 은닉층에서 출력층 뉴런으로 다른 완전연결계층(W_out)이 처리하게 된다.
맥락에 포함시킬 단어가 N개라면 입력층도 N개가 된다.
현재 You와 Goodbye를 가지고 그 사이에 올 단어를 찾고 있다.
여기서 은닉층에 주목하자.
은닉층의 뉴런은 입력층의 완전연결계층에 의해 변환된 값이 되는데, 입력층이 여러개이면 전체를 평균하면 된다.
이를 수식으로 표현하면 아래와 같다.

다음으로 출력층을 보자.
출력층의 뉴런은 총 7개인데, 여기서 중요한 것은 이 뉴런 하나하나가 각각의 단어에 대응한다는 것이다.
즉, 최종적으로 소프트맥스 함수 적용을 통해 확률을 얻는 분류 문제가 된다.
또한, 아래 가중치가 단어의 분산 표현의 정체가 된다.
(7차원 벡터를 3차원 벡터로 압축했다.)

그리고 이 각각의 행벡터는 단어의 의미를 함축하게 된다.
이것이 word2vec의 정체이다.
은닉층의 뉴런 수를 입력층의 뉴런 수보다 적게 해야 한다.
이렇게 해야 은닉층에는 단어 예측에 필요한 정보를 '간결하게' 담게 되고,
결과적으로 밀집벡터 표현을 얻을 수 있다.
이번엔 구현을 위해 계층 관점에서 CBOW 모델을 바라봐보자.

이를 코드로 나타내면 아래와 같다.

현재 random한 값을 가중치 값으로 주었으니, 각자 임의의 값이 나올 것이다.
이제 이걸 데이터 기반으로 학습시켜 word2vec을 구하는 것이다.
모델의 기초 구성을 마쳤으니, 본격적으로 역전파 및 학습에 대해 알아보자.
CBOW 모델의 학습
CBOW 모델의 학습에서는 W_in과 W_out 모두에 단어의 출현 패턴을 파악한 벡터가 학습된다.

이는 대규모 말뭉치로 갈수록 더욱 우리에 직관에 부합한 모델이 되는 것을 확인할 수 있다.
이 이후는 우리가 여태까지 진행한 softmax 와 CEE를 이용한 학습을 수행하면 된다.

그리고 Softmax와 CEE 두 계층을 합치면 Softmax with Loss 계층으로 사용이 가능하다.
따라서 우리가 구현할 신경망은 아래와 같다.

word2vec의 가중치와 분산 표현
지금까지 설명한 것처럼 word2vec에 사용되는 가중치는 다음 두 종류가 있다.
- 입력 측 완전 연결 계층의 가중치(W_in)
- 출력 측 완전 연결 계층의 가중치(W_out)

입력 측은 행 방향, 출력 측은 열 방향으로 특정 단어에 대한 정보가 저장된다.
그렇다면 단어의 분산 표현으로는 뭘 이용하는게 좋을까?
- A안: 입력 측의 가중치만 사용
- B안: 출력 측의 가중치만 사용
- C안: 양쪽 가중치를 모두 사용
C안은 두 가중치를 "어떻게 합치냐"에 따라 또 여러 안이 나온다.
word2vec(특히 skip-gram) 은 A안 사용을 권장한다.
그러므로 우리도 CBOW지만 A안을 사용하도록 한다.
참고로 GloVe의 경우, C안을 사용한다.
학습 데이터 준비
word2vec 학습에 쓰일 학습 데이터를 준비해보자.
맥락과 타깃
우리는 CBOW를 만들고 있다.
즉, 맥락 -> 타깃 형태의 데이터 이용해야 하고, 맥락이 입력되었을 때, 타깃이 출력되는 형태로 구성해야 한다.
그럼 말뭉치에서 '맥락'과 '타겟'을 만드는 작업을 생각해보자.

양 끝 단어(you, .)을 제외한 모든 단어에 적용할 수 있는 함수가 필요하다.
이를 코드로 나타내면 아래와 같다.


이를 그림으로 표현하면 다음과 같다.

그럼 이제 맥락과 타겟을 만드는 함수를 구현할 차례이다.

이를 사용해보자.


각 원소가 여전히 "단어 ID"이다.
이를 원핫 표현으로 변경해보자.
원핫 표현으로 변환
이 변환을 그림으로 표현하면 다음과 같다.

원핫으로 바꾸는 데에는 이 함수를 사용한다.

그럼 지금까지의 과정을 하나로 합쳐보자.

CBOW 모델 구현
우리가 구현할 신경망 모델은 다음과 같다.

이대로 구현을 수행해보자.

초기화 메소드는 인수로 어휘 수(vocab_size)와 은닉층의 뉴런 수(hidden_size)를 받는다.
가중치 초기화 부분에서는 가중치를 2개 생성한다.
이어서 순전파를 구현해보자.

위에서 정의한 대로, 차근차근 구현을 완료했다.
이제 드디어 역전파를 구현할 차례다.
역전파의 구현에는 계산 그래프와 그 공식이 유용하니, 이를 이용해보자.

곱셈은 순전파 시의 입력을 서로 바꿔 기울기에 곱한다.
즉, 0.5가 곱해졌으므로 0.5를 기울기에 곱해준다.
덧셈은 기울기를 '그대로 통과'시킨다.
이를 코드로 구현하면 다음과 같다.

우리는 이미 각 매개변수의 기울기를 인스턴스 변수 grads에 모아뒀다.
이제 forward() 메소드를 한번 호출한 다음 backward() 메소드를 한번 실행하는 것만으로 grads 리스트의 기울기가 갱신된다.
학습 코드 구현
이제 이 CBOW를 학습시켜보자.


보다시피 학습을 거듭할수록 손실이 줄어드는 것을 알 수 있다.
가중치 매개변수를 사용하기 위해 입력 측 MatMul 계층의 가중치를 파악해보자.


word_vecs는 각 단어 id의 분산 표현 역할을 수행한다.
마침내 우리는 단어를 밀집벡터로 나타낼 수 있게 되었다!
학습이 잘 이뤄졌으니 이 분산 표현은 '단어의 의미'를 잘 파악한 벡터 표현으로 되어 있을 것이라 기대할 수 있다.
물론 아직 데이터셋을 충분히 넣지 않았기에, 아쉬움이 있다. 추후 PTB와 같은 큰 데이터셋으로 학습시켜 보자.
word2vec 보충
지금까지 word2vec의 CBOW 모델을 자세히 살펴봤다.
이번 절에서는 지금까지 말하지 못한 word2vec 에 관한 중요한 주제 몇 개를 보충해보자.
- CBOW 모델을 확률 관점으로 보기
- skip-gram vs. CBOW
- 통계 기반 vs. 추론 기반
CBOW 모델과 확률
사실 CBOW 모델은 "조건부 확률"로 표현이 가능하다.
우리가 진행한 문제를 다시 생각해보자.
W_t-1 과 W_t+1 이 있을 때 가운데에 W_t 가 있을 확률이다.

이를 수식으로 표현하면 다음과 같다.

즉 CBOW는 위 식을 모델링하고 있는 것이다.
위 식을 이용하면 CBOW 모델의 손실 함수도 간결하게 표현할 수 있다.
CEE를 적용해보자.

여기서 t_k 가 1일 때만 주어진 로그가 살아남기 때문에, 이 식을 CBOW에선 이렇게 표현할 수 있다.

이 식에서 보듯, CBOW 모델의 손실 함수는 단순히 위에서 정의한 식(확률)에 로그를 취한 다음 음수를 곱했다.
이를 음의 로그 가능도(negative log likelihood)라 한다.
이는 샘플 데이터 하나에 대한 손실 함수이며, 이를 말뭉치 전체로 확장하면 다음과 같다.

CBOW 모델의 학습이 수행하는 일은 이 손실 함수의 값을 가능한 한 작게 만드는 것이다.
그리고 이때의 가중치 매개변수가 우리가 얻고자 하는 단어의 분산 표현인 것이다.
여기에서는 윈도우 크기가 1인 경우만 생각했지만, 다른 크기(또는 m 등의 범용적인 크기)라 해도 수식으로 쉽게 나타낼 수 있다.
skip-gram 모델
앞에서 이야기했듯이, word2vec에는 2개의 모델이 제안되고 있다.
- CBOW (n -> 1, 맥락 -> 타겟)
- skip-gram (1 -> n, 타겟->맥락)
간단하게 skip-gram 모델에 대해 알아보자.

앞서 CBOW에서는 여러개의 입력층과 한개의 출력층을 구현하여 하나의 예상 단어를 출력했다.
하지만 Skip-gram에선 반대로, 한개의 입력층과 여러개의 출력층을 이용해, 하나의 타겟에 이어지는 여러개의 맥락을 추측한다.
이를 그림으로 표현하면 아래와 같다.
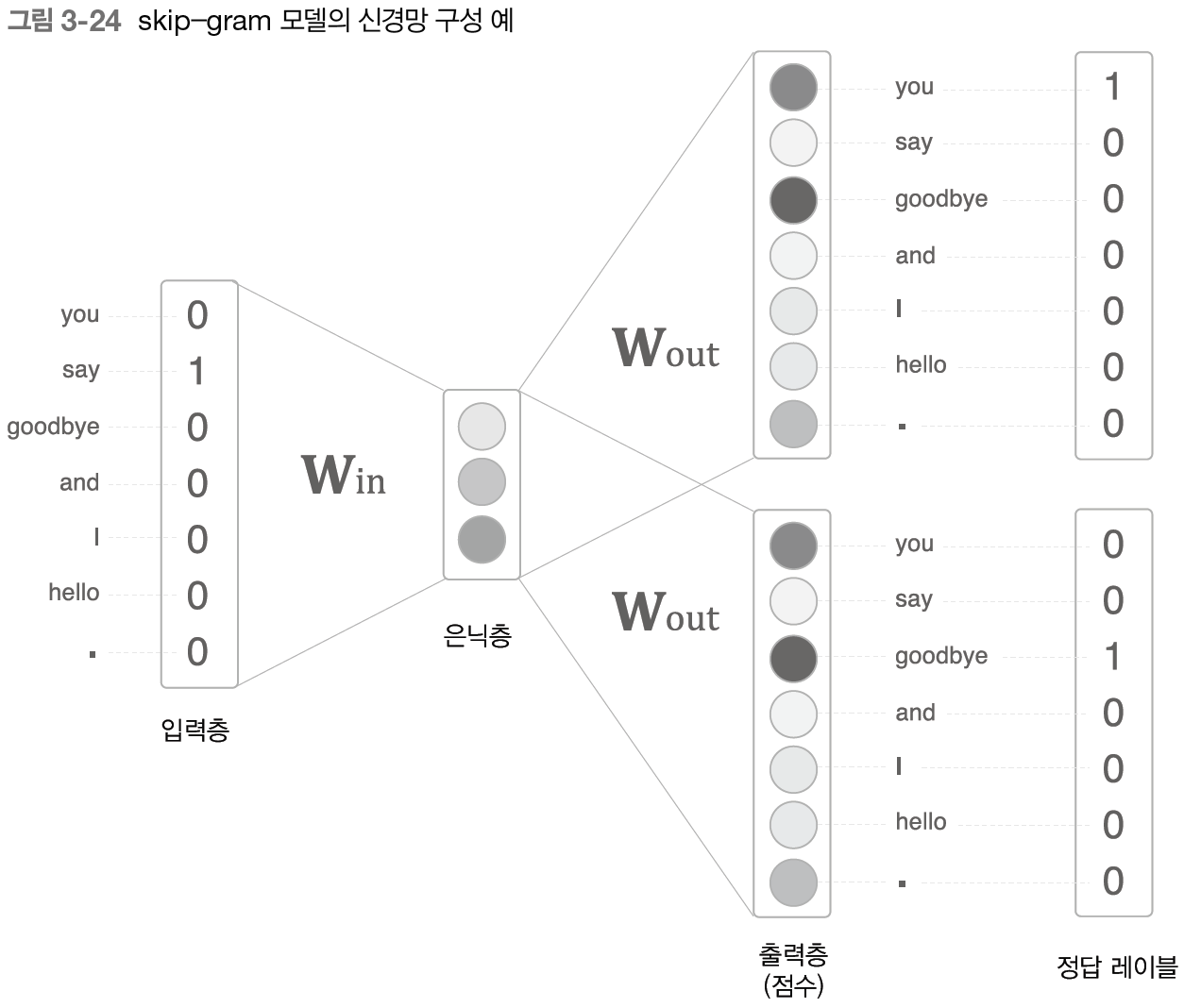
이를 CBOW에서와 같이 확률로 나타내보자.

여기서 skip-gram 모델에서는 맥락의 단어들 사이에 관련성이 없다고 가정(조건부 독립을 가정)하고 다음과 같이 분해한다.

이어서 이 식을 CEE에 적용하여 skip-gram 모델의 손실 함수를 유도해보자.

이렇게 식을 간단하게(컴퓨터가 연산하기 좋게) 만들 수 있었다.
이제 이를 말뭉치 전체로 확장하면 아래와 같은 식이 된다.
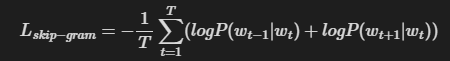
이를 CBOW와 비교하면 다음과 같다.
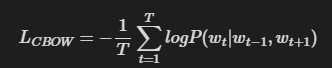
skip-gram은 맥락의 수만큼 추측하기 때문에 그 손실 함수는 각 맥락에서 구한 손실의 총합이어야 한다.
반면 CBOW는 타깃 하나의 손실을 구한다.
그래서 둘 중 어느걸 써야 할까?
그 대답은 skip-gram 모델이라 할 수 있다.
- 단어 분산 표현의 정밀도 면에서 skip-gram이 우수함
- 말뭉치가 커질수록 저빈도 단어나 유추 문제의 성능 면에서 skip-gram 모델이 더 뛰어나다.
다음 절에 단어 분산 표현의 평가에 대해 배웁니다.
반면 CBOW는 skip-gram에 비해 학습 속도 면에서 더 우수한 면을 가지고 있다.
현재 문제에 맞는 적절한 해결책을 선택할 수 있길 바란다.
통계 기반 vs. 추론 기반
지금까지 통계 기반 기법과 추론 기반 기법(특히 word2vec)에 대해 살펴봤다.
이제 이 둘을 비교해보자.
통계 기반 기법
- 전체 통계로 1회 학습하여 단어의 분산 표현 획득
- 새로운 단어의 추가에 취약함.(다시 전체 통계로 1회 학습해야 함)
- 동시발생 행렬 생성
- SVD 수행
추론 기반 기법
- 통계를 미니-배치로 여러번 반복 학습하여 단어의 분산 표현 획득
- 새로운 단어의 추가에 강건함.(기존 가중치부터 이어 학습 시작)
이렇게 차이점에 대해 알아보았으니, 공통(연결)점에 대해 알아보자.
- 두 기법의 성능 차이에는 큰 차이가 없다고 한다.
- 두 기법은 서로 관련되어 있다.
- skip-gram과 (다음 장에서 다룰)네거티브 샘플링을 이용한 모델은 모두 말뭉치 전체의 동시발생 행렬(실제로는 살짝 수정한 행렬)에 특수한 행렬 분해를 적용한 것과 같다.
- 추론 기반 기법과 통계 기반 기법을 융합한 GloVe라는 기법 또한 존재한다.
- 해당 기법은 말뭉치 전체의 통계 정보를 손실 함수에 도입해 미니배치 학습을 수행한다.
이번 장에서 배운 것
- 추론 기반 기법은 추측하는 것이 목적이며, 그 부산물로 단어의 분산 표현을 얻을 수 있다.
- word2vec은 추론 기반 기법이며, 단순한 2층 신경망이다.
- word2vec은 skip-gram 모델과 CBOW 모델을 제공한다.
- CBOW 모델은 여러 단어(맥락)로부터 하나의 단어(타깃)을 추측한다.
- 반대로 skip-gram 모델은 하나의 단어(타깃)로부터 다수의 단어(맥락)을 추측한다.
- word2vec은 가중치를 다시 학습할 수 있으므로, 단어의 분산 표현 갱신이나 새로운 단어 추가를 효율적으로 수행할 수 있다.