[밑바닥부터 시작하는 딥러닝] 퍼셉트론
본 내용은 밑바닥부터 시작하는 딥러닝 1도서를 참고하여 작성되었습니다.
밑바닥부터 시작하는 딥러닝 1 - 예스24
딥러닝 분야 부동의 베스트셀러!머리로 이해하고 손으로 익히는 가장 쉬운 딥러닝 입문서이 책은 딥러닝의 핵심 개념을 ‘밑바닥부터’ 구현해보며 기초를 한 걸음씩 탄탄하게 다질 수 있도록
www.yes24.com
퍼셉트론은 1957년에 고안된 알고리즘으로, 신경망의 기원이 되는 알고리즘이다.
퍼셉트론의 구조 학습은 신경망과 딥러닝으로 나아가는 데 중요한 아이디어를 제공한다.
퍼셉트론으로 가벼운 문제를 풀어보며 딥러닝의 기초를 다져보자.
퍼셉트론이란?
퍼셉트론(Perceptron)은 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 개체를 의미한다. 다만, 퍼셉트론에서 이야기하는 "신호"는 0과 1만 가능하다. 따라서 퍼셉트론 신호는 '흐른다(1)/흐르지 않는다(0)' 두가지 값만 갖게 된다.
예제를 통해 퍼셉트론을 좀 더 이해해보자.

위 그림은 입력으로 2개의 신호를 받고, 출력으로 1개의 신호를 보내는 퍼셉트론의 예이다.
x1과 x2는 입력 신호, y는 출력 신호, w1과 w2는 가중치를 의미한다.
그림의 원을 뉴런 혹은 노드라고 부른다.
입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다.
퍼셉트론은 뉴런에서 보내온 신호의 총합이 정해진 한계를 넘어설 때만 1을 출력하며, 그 한계를 임계값(threshold)이라고 부르고, θ로 나타낸다.
이를 수식으로 나타내면 다음과 같다.
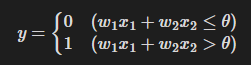
가중치는 각 신호의 강도를 조절하는 기능을 갖게 된다.
즉, 적절한 w1, w2, θ값을 지정하면 원하는 신호를 출력받을 수 있다.
단순한 논리 회로
기본 원리는 꽤나 단순하다. 그럼 이제 이를 이용해서 단순한 논리 회로를 만들어보며 퍼셉트론을 이해해보자.
AND 게이트
AND 게이트를 만족하는 퍼셉트론은 어떻게 구성할 수 있을까?
AND 게이트를 만족시키는 퍼셉트론 구성은 무수히 많다.
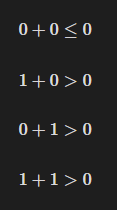
아래 진리표를 보고 직접 식을 구성해보길 바란다.

가령 (w1, w2, θ)가 (1, 1, 1)이면, x1과 x2가 모두 1일때만 AND 게이트의 조건을 만족한다.

NAND 게이트
NAND 게이트의 출력은 AND 게이트에 NOT 연산을 수행한 형태가 된다.
어떻게 해야 NAND 게이트를 구성하는 퍼셉트론이 완성될까?


OR 게이트
OR 게이트는 다음과 같다.
직접 퍼셉트론을 만들어보자.

여기서 퍼셉트론의 매개변수를 정한 것은 컴퓨터가 아니라 우리 인간이 수행했다.
우리는 지금 학습 데이터를 보면서 매개변수의 값을 생각했다.
기계학습 문제는 이 매개변수의 값을 정하는 작업을 컴퓨터가 자동으로 하도록 하며, 이를 학습이라고 한다.
퍼셉트론 구현하기
이제 논리 회로를 파이썬으로 구현해보자.
간단한 구현부터
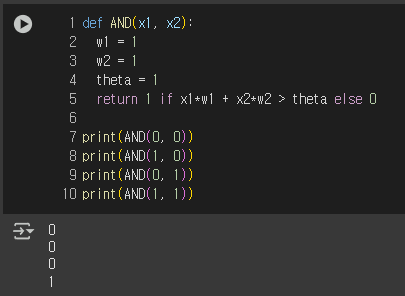
손쉽게 퍼셉트론을 구현할 수 있었다.
하지만, 추후 학습할 신경망과 딥러닝을 위해 numpy를 사용해보자.
가중치와 편향 도입
먼저, θ의 값을 -b로 치환하고, -b를 좌항으로 넘겨주면 식이 다음과 같이 정리된다.
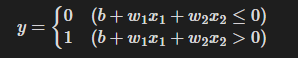
여기서 b를 편향(bias) 이라 하며, w1과 w2는 그대로 가중치라고 부른다.
퍼셉트론은 입력 신호에 가중치를 곱한 값과 편향을 합하여, 그 값이 0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력한다.
그럼 numpy를 이용해서 위 방식으로 다시 구현해보자.

이어서 OR 게이트 또한 구현해보자.
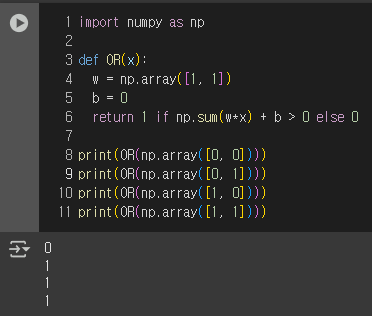
이번엔 NAND 게이트를 구현해보자.

위에서 알 수 있듯이, AND, OR, NAND 게이트는 함수 이름과 가중치, 편향만 다르고, 그 외 나머지는 모두 동일하다는 것을 확인할 수 있다.
퍼셉트론의 한계
도전! XOR 게이트

이번엔 XOR 게이트를 만들어보자.
이 XOR 게이트를 만들려면 어떻게 해야 할까?
시작하기 전에 여태까지 구현한 퍼셉트론의 비밀을 하나 이야기해보려 한다.
우리가 구현한 OR 게이트(1, 1, 0)을 그래프로 시각화해보자.
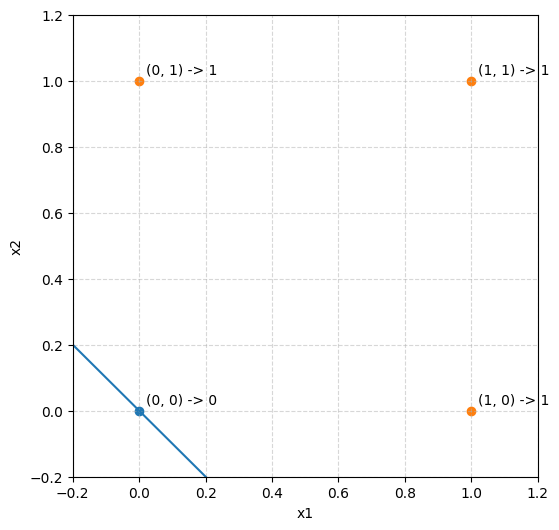
x축을 x1, y축을 x2를 나타낸다고 하면, 이 평면 위에 다음 그래프가 그려지게 된다.

주어진 값을 해당 함수에 대입하면 다음과 같은 결과가 나타난다.

현재 주어진 그래프를 살펴보면, y=-x 그래프가 그려진 것을 확인할 수 있었다.
근데 이게 무슨 상관인가?
우리가 구현한 퍼셉트론에 우리가 구현한 OR 게이트를 대입하여 다시 살펴보자.
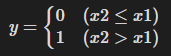
주어진 각 지점에 대하여, 직선 아래에 있는 지점은 0을 출력하고, 직선 위에 있는 지점은 1을 출력하는 형태의 구조가 완성된다.
즉, 위 퍼셉트론은 하나의 직선을 기준으로 평면을 두 공간으로 나누고, 서로 다른 두 공간에 대하여 서로 다른 출력을 내놓게 만드는 것이다!
이를 XOR 게이트에 대입해서 구현해보려 해보자.

위에서 퍼셉트론에 대한 시각화를 시도한 덕분에, 직관적으로 하나의 직선으로 구분하기는 어렵다는 것을 파악할 수 있다.
이와 같은 접근을 "선형 분리" 라고 하며, 관련 내용은 "퍼셉트론 수렴 정리"를 참고해주시길 바랍니다.
선형과 비선형
우리는 방금 직선 형태로는 XOR을 구현하긴 어렵다는 것을 알 수 있었다.

이렇게 곡선을 그린다면, 쉽게 구분할 수 있을 것 같은데, 퍼셉트론으로 곡선을 그리는 방법은 없을까?
다층 퍼셉트론이 출동한다면?
안타깝게도 단층 퍼셉트론으로는 XOR 게이트를 표현할 수 없다.
하지만, 다층 퍼셉트론이 출동한다면 어떨까?
기존 게이트 조립하기
흔히 컴퓨터공학의 디지털 논리 회로 시간에 XOR 게이트를 NAND게이트만으로 만드는 간단한 예제를 진행하곤 했는데, 이번엔 OR과 AND, NAND 연산을 모두 이용해서 XOR 게이트를 만들어보자.

NAND와 OR 연산의 결과를 AND 하면 원하는 (0, 1, 1, 0)을 출력하는 게이트를 만들 수 있을 것 같다.
이쯤에서 다층 퍼셉트론을 도입해보자.
XOR 게이트 구현하기 - 다층 퍼셉트론(Multi-Layer Perceptron, MLP)
다층 퍼셉트론은 퍼셉트론을 여러층에 걸쳐 쌓아올린 형태의 네트워크를 의미한다.

위 이미지에서는 다음과 같은 동작을 수행할 것이다.
- 0층의 두 뉴런이 입력 신호를 받아 1층의 뉴런으로 신호를 보낸다.
- 1층의 뉴런이 2층의 뉴런으로 신호를 보내고, 2층의 뉴런은 이 입력 신호를 바탕으로 y를 출력한다.
이를 이용해서 XOR 게이트를 구현해보자.

이로써 다층 퍼셉트론을 이용해 XOR 게이트를 구현할 수 있었고, 퍼셉트론의 비선형 영역으로의 확장 가능성을 살펴볼 수 있었다.
이번 장에서 배운 것
- 퍼셉트론은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.
- 퍼셉트론에서는 '가중치'와 '편향'을 매개변수로 설정한다.
- 퍼셉트론으로 AND, OR 게이트 등의 논리 회로를 표현할 수 있다.
- XOR 게이트는 단층 퍼셉트론으로는 표현할 수 없다.
- 2층 퍼셉트론을 이용하면 XOR 게이트를 표현할 수 있다.
- 단층 퍼셉트론은 직선형 영역만 표현할 수 있고, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.