[논문 리뷰] Proximal Policy Optimization Algorithms

AI Repository/DRL

[논문 리뷰] Proximal Policy Optimization Algorithms

조금씩 차근차근 2025. 10. 1. 00:01

본 글은 "Proximal Policy Optimization Algorithms” (Schulman, Wolski, Dhariwal, Radford, Klimov, 2017)를 읽고 리뷰한 내용입니다.

Proximal Policy Optimization Algorithms

We propose a new family of policy gradient methods for reinforcement learning, which alternate between sampling data through interaction with the environment, and optimizing a "surrogate" objective function using stochastic gradient ascent. Whereas standar

arxiv.org

나의 요약

정책 업데이트 시 기존 정책에서 크게 달라지는 걸(발산) 막기 위해 CPI(보수적 정책 iteration)라는 기법이 있다.
- CPI는 성능이 하락하지 않도록 정책을 보수적으로 섞어 업데이트하면서, 성능의 하한을 보장하는 기능을 수행한다.
- 그런데, CPI를 사용하더라도 iteration되면 정책이 크게 달라질 수 있다.
PPO는 여기서 정책이 크게 달라지지 않도록, 달라지는 범위 자체를 클리핑으로 제한한다.
- 이때, 정책 변화를 직접 건드리지 않고, 이전 정책-갱신 정책 간 확률비가 지나치게 커지지 않도록 목적 함수를 건드린다.
- PPO의 클리핑은 큰 업데이트를 안정화할 뿐, 탐색/신호 부족을 해결해주진 않는다.
PPO는 연속 정책 환경에서 정책이 이전과 지나치게 달라지는 문제를 클리핑을 통해 해결한 알고리즘이다.

서문

다양한 강화학습용 신경망 근사 함수가 제안되어왔다.
DQN과, 바닐라 Policy Gradient, TRPO가 많이 쓰였다.
그러나 확장 가능성(데이터 모델과 병렬 구현) 데이터 효율성, 그리고 강건성(하이퍼파라미터 튜닝 없이도 다양한 문제에서 성공적으로 작동하는 것)을 모두 갖춘 방법을 개발하는건 어렵다.
함수 근사를 사용하는 Q-Learning은 많은 단순한 문제에서도 실패하고, 그 원리를 이해하기 어렵다.
바닐라 policy gradient는 데이터 효율성과 강건성이 떨어진다.
TRPO는 상대적으로 복잡하고, dropout과 같은 노이즈를 포함하는 아키텍처나 정책-가치함수 간, 혹은 보조 과제와의 매개변수 공유와는 호환되지 않는다.
PPO는 데이터 효율성과 안정적인 성능을 유지하면서도 first-order optimization만 사용하는 알고리즘을 도입한다.
- 클리핑된 확률 비율(clipped probability ratios)을 사용하는 새로운 objective function을 제안한다.
- 이는 정책 성능에 대한 보수적 추정치(즉, 하한선)를 형성한다.
- 정책을 최적화하기 위해, 정책으로부터 데이터를 샘플링한 뒤, 샘플링된 데이터에 대해 여러 차례의 최적화를 수행하는 과정을 번갈아 실행한다.

강화학습(RL)에서는 보통 maximize할 대상이므로 objective function 이라는 표현을 더 자주 쓰고, 딥러닝 일반에서는 minimize할 대상이라 loss function 이라는 표현을 더 많이 쓴다.

다양한 형태의 surrogate objective 들의 성능을 비교한 결과, clipped probability ratios을 사용하는 버전이 제일 우수했다.

continuous control 과제에서 다른 알고리즘보다 훨씬 좋았다.
Atari 환경에서는 sample complexity 측면에서 A2C보다 훨씬 뛰어났고, ACER와는 비슷한 성능을 보였으나 구조적으로는 훨씬 단순하였다.

사전지식 1: Policy Optimization

정책경사법 (Policy Gradient Methods)

정책 경사법(policy gradient methods)은 정책 경사의 estimator를 계산하고, 이를 확률적 경사 상승법(stochastic gradient ascent algorithm)에 대입하여 동작한다. 가장 흔히 사용되는 gradient estimator는 다음과 같은 형태를 가진다.

pi: 정책(확률적)
A: advantage 추정치
E: 유한한 batch 내 샘플에 대한 empirical average(실무적인 평균)

자동 미분을 이용한 구현에서는 기울기가 "정책 경사 추정치가 되도록 하는 objective function"을 구성한다.
추정치 g햇은 이 objective function을 미분하여 얻어진다.

이 손실함수 L에 대해 동일한 trajectory(궤적)을 사용하여 여러 번 최적화 단계를 수행하는 것은 매력적으로 보이지만, 이론적으로도 정당화되기 어렵고 실무적으로도 종종 정책이 지나치게 크게 업데이트되는 문제를 야기한다.

사전지식 2: Trust Region Methods

TRPO에서는 목적 함수(Surrogate Objective)를 최대화하되, 정책 업데이트 크기에 대한 제약 조건을 둔다.

단, 아래 조건을 만족시켜야 한다.

여기서 θ_old는 갱신 이전의 정책 파라미터 벡터를 뜻한다. 목적함수에 대해 선형 근사, 제약에 대해 이차 근사를 한 뒤 공액 기울기(Conjugate Gradient, CG) 알고리즘을 사용하면, 이 문제를 효율적으로 근사적으로 풀 수 있다.

TRPO를 정당화하는 이론은 사실 제약 대신 패널티를 쓰는 방식을 제안한다. 즉 어떤 계수 β에 대해 다음의 비제약 최적화 문제를 푸는 것이다.

이는 (평균 KL이 아니라) 상태들에 대한 KL의 최댓값을 사용해 계산되는 어떤 대리 목적함수(surrogate objective)가 정책 π의 성능에 대한 하한(보수적 경계)을 형성한다는 사실에서 비롯된다. TRPO가 패널티 대신 하드 제약을 쓰는 이유는, 서로 다른 문제들 전반에서(심지어 학습이 진행되며 특성이 변하는 단일 문제 내부에서도) 잘 동작하는 단일 β 값을 고르기가 어렵기 때문이다.

따라서 TRPO의 단조 개선 특성을 모방하는 1차(gradient 기반) 알고리즘을 달성하려면, 고정된 패널티 계수 β를 택해 위 식의 패널티가 붙은 목적함수를 SGD로 최적화하는 것만으로는 충분하지 않다는 것이 실험적으로 드러났으며, 추가적인 수정이 필요하다.

클리핑된 대체 목적 함수 (Clipped Surrogate Objective)

rt(θ)를 확률비(우도비)로 정의하자.

따라서 r(θ_old)=1이다.
TRPO는 다음의 ‘대리(surrogate) 목적함수’를 최대화한다.

여기서 윗첨자 CPI는 이 목적함수가 제안된 보수적 정책 반복(conservative policy iteration) 을 가리킨다. 제약이 없다면 LCPI를 최대화하는 것은 지나치게 큰 정책 갱신으로 이어질 수 있다. 따라서 이제rt(θ)가 1에서 멀어지도록 만드는 정책 변화를 페널티 주도록 목적함수를 어떻게 수정할지 살펴본다.

논문에서 제안하는 주된 목적함수는 다음과 같다.

여기서 ϵ은 하이퍼파라미터로, 예를 들어 ϵ=0.2이다.

이 목적함수의 동기는 다음과 같다.

min 내부의 첫 항은 LCPI이다.
min 내부의 두 번째 항 clip * ⁡A^t는 확률비를 클리핑하여, r_t가 구간 [1−ϵ,1+ϵ] 밖으로 벗어나려는 유인을 제거한다.
마지막으로, 클리핑하지 않은 항과 클리핑한 항의 최소값을 취하므로 최종 목적함수는 언클립(unclipped) 목적함수에 대한 하한(즉, 보수적 경계)이 된다.

이 방식에서는, 목적함수가 개선되는 방향일 때만 확률비의 변화를 무시하고, 목적함수를 악화시키는 방향일 때는 그 변화를 포함한다.

θold 주변(즉 r=1)에서 1차(선형) 수준까지는 L_{CLIP}(θ)=L_{CPI}(θ)이지만, θ가 θold에서 멀어질수록 두 함수는 달라진다.

아래 그림은 L_CLIP의 단일 항(즉, 단일 t)을 그린 것으로, 어드밴티지가 양수인지 음수인지에 따라 확률비 r가 1−ϵ 또는 1+ϵ에서 클리핑됨을 보여준다.

다음 그림들은 확률비 r에 대한 함수로서 대리 목적함수 L_{CLIP}의 한 항(즉, 단일 타임스텝)을 나타낸 것이다.

왼쪽은 어드밴티지가 양수일 때, 오른쪽은 음수일 때의 경우다.
각 플롯의 빨간 원은 최적화의 시작점, 즉 r=1을 의미한다.

L_CLIP은 이러한 항들을 여러 개 합한 값임에 유의하라.

위 그림은 대리 목적함수 L_CLIP에 대한 또 다른 직관을 제공한다.
연속 제어 문제에서 (곧 소개할) 근접 정책 최적화(Proximal Policy Optimization)로 얻은 정책 갱신 방향을 따라 보간(interpolate)하면서, 여러 목적함수가 어떻게 변하는지를 보여준다.
이를 통해 L_CLIP이 정책 갱신이 지나치게 커지는 경우에 패널티를 부과하면서 L_CPI의 하한(lower bound)을 이룬다는 것을 확인할 수 있다.

x축: Linear interpolation factor
y축: 각 값들

Linear interpolation factor

두 지점 사이를 얼마나 섞을지를 정하는 가중치.
예전 파라미터 old와 현재 파라미터 new를 섞는다면

라고 표현하여 섞는다.

또는,

이라면

를 의미한다.

갱신된 정책(alpha = 1)은 초기 정책(alpha = 0)과의 KL 발산(파란 색 선)이 약 0.02이며, 이 지점에서 L_{CLIP}(빨간 색 선)이 최대가 된다.

적응형 KL Penalty 계수 (Adaptive KL Penalty Coefficient)

클리핑된 대리 목적함수의 대안으로(또는 그에 추가로) KL 발산에 패널티를 두고, 매 정책 갱신마다 KL 발산의 목표값 d_{targ}을 달성하도록 패널티 계수(β)를 적응적으로 조정하는 방법이 있다.
논문의 실험에서는 KL 패널티 방식이 클리핑된 대리 목적함수보다 성능이 떨어졌지만, 중요한 기준선(baseline)이므로 여기에 작성했다.

가장 단순한 형태의 알고리즘에서는 각 정책 갱신마다 다음을 수행한다

여러 epoch에 걸친 미니배치 SGD로, KL 패널티가 붙은 다음 목적함수를 최적화한다.

다음 식을 계산한다.

갱신된 β는 다음 정책 갱신에 사용된다.
이 방식에서는 때때로 KL 발산이 d_targ와 상당히 다르게 나오는 업데이트가 나타나지만, 이런 경우는 드물고 β는 빠르게 조정된다.
위의 1.5와 2라는 값은 경험적으로 정했지만, 알고리즘은 이에 크게 민감하지 않다.
β의 초기값 역시 또 하나의 하이퍼파라미터이지만, 알고리즘이 이를 빠르게 조정하므로 실제로는 중요하지 않다.

알고리즘

이전 절에서 제시한 대리 손실(surrogate loss)들은 전형적인 정책 그래디언트 구현에 약간만 수정하면 계산과 미분이 가능하다.
자동 미분을 사용하는 구현에서는 L_{PG} 대신 L_CLIP 또는 L_KLPEN 손실을 구성하고, 이 목표함수에 대해 확률적 경사 상승(SGA)을 여러 단계 수행하면 된다.

분산을 줄인 어드밴티지 함수 추정기를 계산하는 대부분의 기법은 학습된 상태 가치 함수 V(s)를 사용한다. 예를 들어, 일반화 어드밴티지 추정(GAE) 이나 A3C의 유한 지평선(finite-horizon) 추정기가 그렇다.

정책과 가치 함수가 파라미터를 공유하는 신경망 아키텍처를 사용할 경우, 정책 대리 목적함수와 가치 함수 오차 항을 결합한 손실 함수를 사용해야 한다.
여기에 과거 연구에서 제안된 바와 같이 충분한 탐색을 보장하기 위해 엔트로피 보너스를 추가할 수 있다.

이 항들을 결합하면 각 반복에서 (근사적으로) 최대화하는 다음의 목적함수를 얻는다.

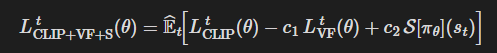
여기서 c_1, c_2는 계수이고, S는 엔트로피 보너스를 의미하며, L_t^{VF}는 제곱 오차 손실이다.

정책 그래디언트 구현의 한 방식은 정책을 T개의 타임스텝 동안만 실행하고(에피소드 길이보다 훨씬 짧음), 수집한 샘플로 갱신을 수행하는 것이다.
이 방식은 T를 넘어서는 정보를 보지 않는 어드밴티지 추정기가 필요하다.
A3C 논문에서 사용된 추정기는 다음과 같다.

여기서 t는 길이 T인 궤적 구간 내에서 [0, T]의 시간 인덱스를 나타낸다. 이를 일반화하면, lambda=1일 때 아래 식으로 환원되는 절단형(truncated) GAE를 사용할 수 있다.

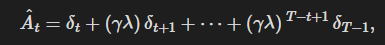
여기서

길이 궤적 구간을 사용하는 근접 정책 최적화(PPO) 알고리즘은 아래와 같다. 각 반복마다, N개의 (병렬) 액터가 T 타임스텝의 데이터를 수집한다. 그런 다음 이 NT개의 타임스텝 데이터로 대리 손실을 구성하고, 미니배치 SGD(또는 보통은 더 나은 성능을 위해 Adam을 사용할 수 있음)로 K 에폭 동안 최적화한다.

실험

먼저, 서로 다른 하이퍼파라미터 설정하에서 여러 대리 목적함수를 비교한다. 여기서는 대리 목적함수 L_{CLIP}을 몇 가지 자연스러운 변형 및 제거(ablated) 버전들과 비교한다.

클리핑/패널티 없음

클리핑

KL 패널티(고정 또는 적응형)

KL 패널티의 경우, 섹션 4에서 설명한 목표 KL 값 d_targ을 사용하는 적응형 계수를 쓰거나, 고정된 계수 β를 사용할 수 있다. 또한 로그 공간에서의 클리핑도 시도했지만, 성능 향상은 없었다.

각 알고리즘 변형마다 하이퍼파라미터 서치를 수행해야 하므로 계산 비용이 낮은 벤치마크를 선택했다.

OpenAI Gym의 MuJoCo 내 7개의 시뮬레이션 로보틱스 과제를 사용
각 과제마다 100만 타임스텝 학습
하이퍼 파라미터는 다음과 같았다.

정책 표현으로는 완전연결 MLP(은닉층 2개, 각 64 유닛, tanh 비선형)를 사용했고, 가우시안 분포의 평균을 출력하도록 했다(표준편차는 가변).

각 알고리즘은 7개 환경 모두에서 3개 시드로 실행했다.
- 알고리즘의 각 실행(run)은 마지막 100 에피소드의 평균 총 보상으로 점수를 매겼다.
- 환경별로 점수를 이동/스케일하여 무작위 정책의 점수는 0, 해당 환경에서의 최고 결과는 1이 되도록 정규화했고, 21개 실행(7환경 × 3시드)에 대해 평균을 내어 알고리즘별 하나의 스칼라 점수를 만들었다.

위 표는 결과이다.
클리핑이나 패널티가 없는 설정의 점수가 음수인 데 유의하라.
이는 한 환경(half cheetah)에서 매우 낮은 점수가 나와 초기 무작위 정책보다도 나빠졌기 때문이다.