[개발자를 위한 필수 수학] 로지스틱 회귀와 분류
본 내용은 “개발자를 위한 필수 수학” 도서를 참고하여 작성되었습니다.
개발자를 위한 필수 수학 - 예스24
개발자를 구원하는 실용 수학 안내서기초 수학부터 회귀 모델, 신경망 그리고 진로 조언까지 데이터 과학, 머신러닝, 통계학에서 탁월한 능력을 발휘하는 데 필요한 수학을 이해하고 여러분의
www.yes24.com
시작하기 전에 - 오해 풀기
로지스틱 회귀는 회귀 알고리즘이 아닌 분류 알고리즘이다.
- 회귀
- 임의의 실숫값을 예측하는 것
- 분류
- 범주 중 하나를 예측하는 것
분류 알고리즘의 핵심은 결과를 분류 확률로 변환하는 것이다.
임곗값을 이용해 이산형 값으로 변경도 가능하다.
그럼 지금부터 분류 알고리즘인 로지스틱 회귀에 대해 알아보자.
특징
로지스틱 회귀는 구현하기 쉽고 이상치와 기타 데이터 문제에 상당히 탄력적이다.
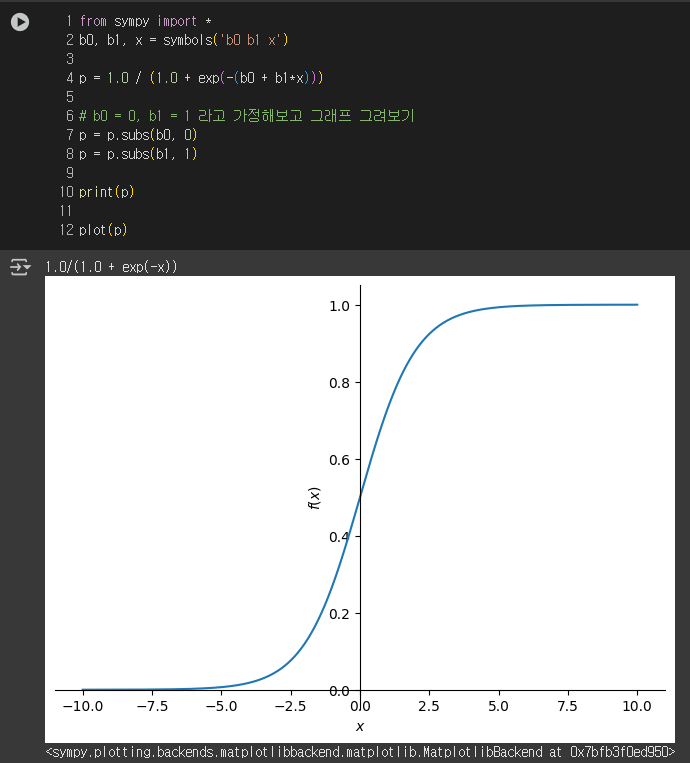
로지스틱 함수와 시그모이드 함수
시그모이드 함수
시그모이드 함수는 S자 형태를 보이는 함수들의 전체 집합을 의미한다.
하지만 일반적으로 아래 로지스틱 함수와 같은 의미로 사용된다.
엄밀하게 구분해야 할 경우, 따로 명시를 해주는 것이 좋다.

로지스틱 함수
S자 형태를 띄는 함수 중 다음 함수를 의미한다.
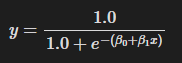
이때 지수에 있는 이 선형 함수(b0 + b1*x)를 로그 오즈(log-odds) 함수라고 부른다.
선형 회귀와 마찬가지로 로지스틱 회귀를 둘 이상의 입력 변수(x_1, x_2, ...x_n) 으로 확장 가능하다.
그러면 공식은 다음과 같은 형태를 띄게 된다.
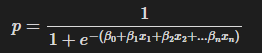

기본 정의를 살펴봤으니, 이제 로지스틱 회귀를 학습하는데 사용하는 손실 함수와 학습 방법이 궁금해질 것이다.
이에 대해 자세히 알아보기 전에, 확률을 나타내는 용어인 ‘확률’, ‘가능도(우도)’, ‘오즈’에 대해 알아보자.
확률
- 어떤 사건이 일어날 것이라고 믿는 정도
- 미래 시점의 관점을 나타낸다.
- 상호 배타적인 모든 확률의 합이 1이 되어야 한다.
가능도(우도)
- 이미 발생한 사건의 빈도를 측정하는 것
- 과거 시점의 관점을 나타낸다.
- 상호 배타적인 모든 가능도의 합이 1이 아닐 수 있다.
확률과 가능도를 같은 의미로 쓰는 경우도 있는데, 둘은 엄연히 다른 종류이다.
오즈

오즈는 한국어로 '승산'으로 번역되며("승산이 있다" 할때 그 승산이 맞다!), 성공확률/실패확률로 계산된다.
오즈가 2.0이면 “어떤 사건이 일어날 확률이 일어나지 않을 확률보다 두배 더 높다”라고 말할 수 있으며, 주로 도박이나 베팅에서 주관적인 믿음을 정량화하는데 사용한다.
로그 오즈를 이용한 로지스틱 회귀, Bayes Factor 를 포함한 베이즈 통계에서 사용한다.
앞으로 자주 나올 용어라서 다시 한번 정의해두었다.
이제 본격적으로 로지스틱 회귀의 훈련을 시도해보자.
최대 우도(가능도) 추정(MLE)
앞서 선형 회귀에서 살펴봤듯이, 먼저 머신러닝을 위해선 다음 세가지가 정의되어야 한다.
- 손실 함수
- 손실 함수의 최솟값을 찾는 방법
- 데이터가 해당 모델과 잘 어울리는지를 판단하는 기준
입력과 출력 데이터를 통해, 현재 데이터를 가장 잘 나타내는 로지스틱 함수의 b_1과 b_1 계수를 찾아야 한다.
선형 회귀에서는 최소 제곱법이라는 좋은 도구가 있었지만, 로지스틱 회귀에서는 해당 방법이 동작하지 않는다.
로지스틱 회귀에서는 최대 우도 추정법(MLE)을 사용한다.
최대 우도 추정
용어가 어색해서 난해하게 들릴 수 있는데, 차근차근 가능도의 정의에 대해서 다시 생각해보자.
가능도는 이미 발생한 사건의 빈도를 측정한다.
x가 3일 때, 0이 3번 등장하고 1이 7번 등장했다고 가정하자.
그렇다면 로지스틱 함수는 x에 3을 입력받았을 때, 몇을 출력하는 게 가장 관측된 데이터를 출력할 가능성이 높을까?
70%의 확률로 1을 출력하는 것이 가장 관측된 데이터를 출력할 가능성을 높힐 것이다.
이렇게 단일 매개변수 x에 대하여 우도 추정을 진행했다.
그렇다면 이 우도 추정이 모든 x에 대하여 실제 데이터를 가장 잘 반영하는 기준은 뭘까?
과거 확률론에서 학습하였던 결합 확률 개념을 도입함으로써 실마리를 찾을 수 있다.
과연 이 예측이 이전의 예측에 영향을 받는 개념인가?
아니다. 즉 각 예측이 독립시행으로 진행된다.
따라서 다음과 같은 식이 성립 가능하다.
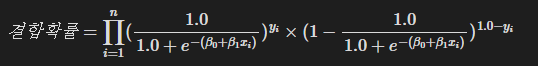
(지수승은 출력값이 0이 나온다면 곱셈 결과에 영향을 반대로 주기 위한 트릭이다. 아래 코드와 연관지어 지수에서 참(1) 및 거짓(0) 을 처리하는 방식을 잘 이해해보자.)

따라서 정의역 내 모든 x에 대하여 우도를 추정할 수 있었다.
즉, 최대 우도 추정이란, 로지스틱 함수를 모든 입력 데이터 x에 대하여 관측된 데이터를 출력할 가능성이 가장 높도록 만드는 것이다.
로지스틱 함수는 기본적으로 b를 매개변수로 갖는 함수이기 때문에, 우리는 최대 우도 추정을 손실 함수로 갖는 경사 하강법을 통해 적절한 b를 찾는 과정을 수행한다.
최적화 - log 연산
앞서 선형회귀에서 행렬 분해 기법을 학습하면서, 소수점 연산에 곱셈이 가해질 경우 오차가 커지는 문제가 발생한다는 것을 학습했다.
이 곱셈 연산의 오차를 줄이는 방법이 없을까?
곱셈 연산 대신 덧셈을 사용하면, 곱셈에 비해 오차가 많이 줄어들 것이다.
여기서 우리는 양변에 로그를 취함으로써 곱셈 연산을 덧셈 연산으로 바꿀 수 있게 된다.
공식으로 표현하면 다음과 같다.

이 식에 대해서 b0과 b1에 대한 편도함수를 구하고 경사 하강법을 수행하면 우리가 원하는 최적의 b0, b1값을 구할 수 있게 될 것이다.

다변수 로지스틱 회귀
그럼 이제부터 로지스틱 회귀를 직접 적용해보기 위해, 가정과 조작으로 떡칠된 데이터를 가지고 데이터 분석을 시도해보자.

이 데이터 셋을 사용해, 직원의 퇴사 여부를 예측하는 로지스틱 회귀 학습을 시도해보자.
이전에 이야기한 것처럼 로지스틱 회귀는 다변수로 확장 가능하고, 현재 매개변수가 4개이므로 다음과 같이 로지스틱 회귀 함수를 정의할 수 있다.

sex, age, promotions, years_employed 에 대해 베타 계수를 각각 만들고, 출력 변수 did_quit을 출력값으로 두어 로지스틱 회귀 함수를 정의해보자.
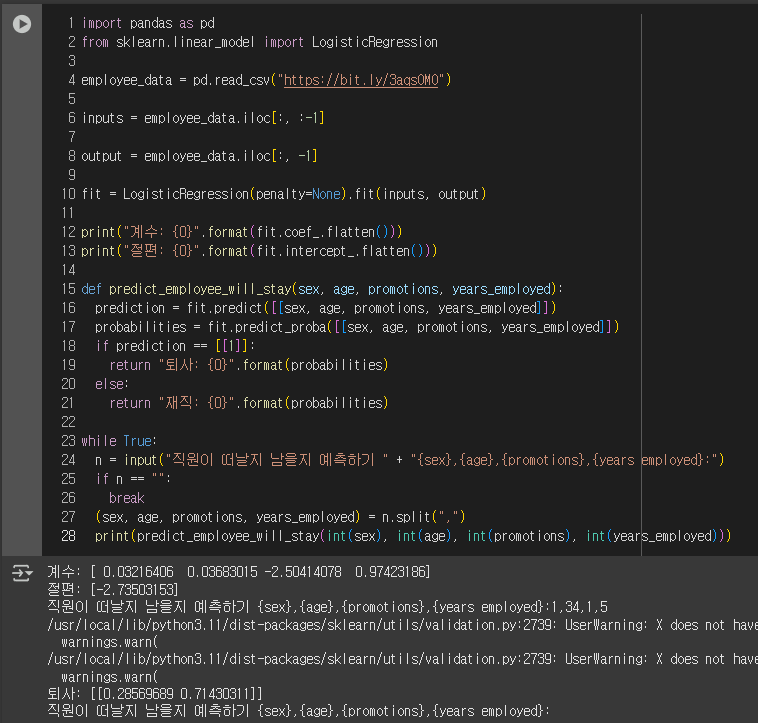
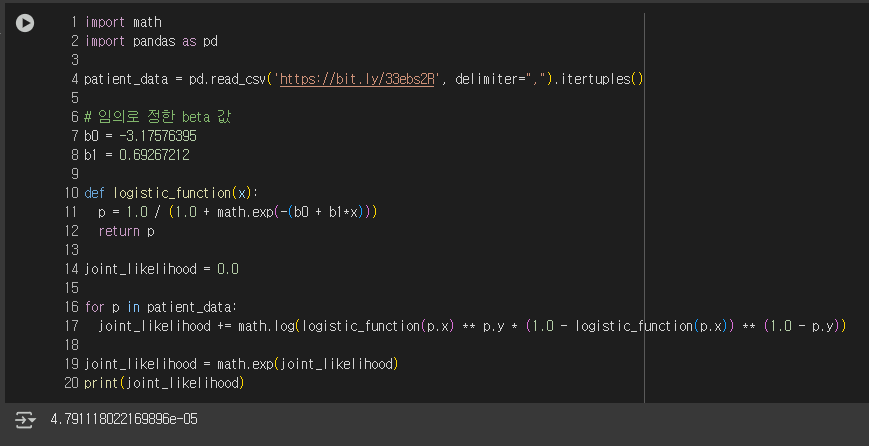
결과를 보면 sex와 age 매개변수에 대한 beta 값은 0에 가까워, 예측에 거의 영향을 끼치지 않는다.
하지만 promotions와 years_employed는 -2.504와 0.97로 꽤 가중치가 크다는 것을 확인했다.
사람을 분류할 때 주의하세요!
사람에 대한 데이터를 수집하고, 이를 사용해 마구잡이로 예측하지 마라. 데이터 프라이버시 문제가 발생할 수 있을 뿐만 아니라 모델이 차별적이라고 밝혀질 경우 법적 및 홍보 문제가 발생할 수 있다.
예를 들어, 머신러닝 훈련을 통해 인종, 성별과 같은 입력 변수에 가중치가 부여될 수 있다.
그 결과, 인구 통계학적 특성에 따라 채용이 거부되거나 대출이 거절되는 등 바람직하지 않은 결과가 초래될 수 있다.
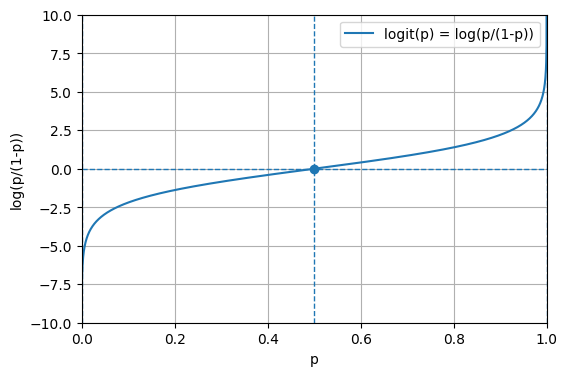
로그 오즈 이해하기
이제 로지스틱 회귀가 수학적으로 어떻게 구성되는지 이야기해보자.
1900년대부터 수학자들은 선형 함수를 취해 출력이 0과 1 사이가 되도록 스케일을 조정해 확률을 예측하고 싶어했다. logit function(로짓 함수)라고도 불리는 로그 오즈는 이러한 목적을 갖고 있기 때문에 로지스틱 회귀에 적합하다.
일단 로지스틱 함수의 설명을 다시 봐보자.

이때 지수에 있는 이 선형 함수(b0+b1*x)를 로그 오즈(log-odds)함수라고 부른다고 했는데, 이 선형 함수에 log는 눈씻고 봐도 찾아볼수가 없다. 왜 이 beta로 이루어진 선형 함수를 로그 오즈라고 하는걸까?
오즈의 정의를 다시 살펴보자.

오즈가 1이면 사건이 일어나지 않을 가능성과 사건이 일어날 확률이 동등하고, 이는 1 기준으로 비선형적으로 구성된다. 이는 사람이 이해하기 비직관적인 구조를 갖게 되는데, 이를 양변에 로그를 취하면 (1/2, 0) 에 대칭인 함수를 만들 수 있다.
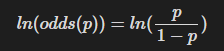
로지스틱 함수에 로그 오즈를 대입하면, 다음과 같은 결과가 된다.

로지스틱 함수의 출력값을 확룰로 표현할 수 있게 되는 것이다.
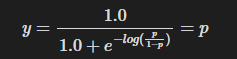
로그 오즈라는 비선형 함수를 x의 일차결합으로 표현하는 원리는 완벽히 이해하지 못해 관련 내용을 링크로 남겨둡니다.
https://www.youtube.com/watch?v=ARfXDSkQf1Y
https://en.wikipedia.org/wiki/Generalized_linear_model
R^2 - 로지스틱 회귀에서의 결정 계수
우리는 선형 회귀를 학습하며 상관 계수와 결정 계수라는 개념을 통해, 해당 데이터가 실제로 상관관계를 갖고 있는게 맞는지 검증하는 과정을 수행했다.
당연하게도 로지스틱 회귀에도 해당 과정이 존재하며, 로지스틱 회귀에서는 다음과 같은 수식을 통해 구한다.

해당 수식의 경우, 선형 회귀의 R^2 과 가장 유사하여 자주 쓰이며, 맥패든의 수도 R^2 이라고 불린다.
이제 "훈련 전 로그 가능도"와 "훈련 후 로그 가능도"를 어떻게 구하는지 알아보자.
훈련 후 로그 가능도
훈련 후 로그 가능도는 우리가 MLE를 공부하며 결합확률을 구할 때 이용했던 가능도의 최댓값에 로그를 취한 것을 의미한다.
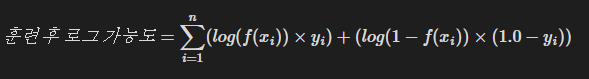
최종적으로 구한 b0와 b1을 이용해 가능도를 구하는 연산을 적용하면 된다.
이 또한 log 연산을 먼저 수행한 뒤 가능도값을 구하면 실수 오차를 줄일 수 있다.

훈련 전 로그 가능도
훈련 전 로그 가능도는 다음과 같은 수식을 통해 구할 수 있다.
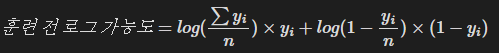
이는 입력 변수를 사용하지 않고 단순히 참(즉, y=1)인 표본의 수를 모든 표본의 개수로 나눈 값을 사용한다. 0이 아닌 1만 합계에 포함되는 것을 확인하자.
이를 구하는 코드는 다음과 같다.

그리하여 최종적으로 R^2을 구하는 코드는 다음과 같다.

p 값 - 이 결정 계수가 우연이 아닌가?
선형회귀와 마찬가지로, R^2을 구했다고 끝이 아니다. 실제 연관성 때문이 아니라 우연히 이 데이터를 볼 가능성이 얼마나 되는지 또한 조사해야 한다. 즉, p-value가 필요하다.
이를 위해서 로지스틱 회귀에서는 카이제곱 분포를 사용한다.

훈련/테스트 분할
앞서 선형회귀에서도 살펴보았지만, 데이터 과학자는 입력변수의 개수가 매우 많을 때는 모든 분석에 대해 결정 계수와 p-value를 이용한 검증보단, 머신러닝에 맞는 베이지안 통계학을 적용한 검증 방식을 더욱 선호한다.
그러므로, 다시 전기톱을 꺼내들 때다.

이렇게 세개의 훈련에 대한 정확도 평균과 표준편차를 구했다.
하지만 분류 문제에선 정확도(Accuracy) 개념이 잘 쓰이지 않는데, 그 이유에 대해 알아보자.
오차 행렬, F1-score
지금부터 하나의 예제로 이야기를 풀어나가보겠다.
'마이클'이라는 이름을 가진 사람들이 직장을 그만두는 것을 관찰한 모델이 있다고 가정해보자. 예제를 단순화하기 위해 모덴은 단순히 이름이 '마이클'인 사람이 직장을 그만둘 것이라 예측을 하기 시작했다.
지금부터 정확도(Accuracy)가 문제가 되는 경우를 살펴보자.
이름이 '마이클'인 직원 한명과 '샘'이라는 이름을 가진 직원 99명, 총 100명이 있다고 가정해보자.
모델은 마이클이 그만둘 것이라 잘못 예측했고, 실제로는 수많은 샘 중 한명이 회사를 그만두었다.
모델의 정확도는 몇인가?
100명의 직원 중 단 두명만 잘못 예측했기 때문에, 정확도는 98%이다!
(98명의 샘은 그만두지 않았다. 그만둘거라 예측했던 마이클도 그만두지 않았고, 그만두지 않을 거라 예측했던 샘은 그만두었다.)
이처럼 관심있는 이벤트가 드물게 발생하는 불균형한 데이터의 경우, 정확도 지표는 분류 문제에 대해 큰 오해를 일으킬 수 있다.
이를 larger set에 지배를 당한다고 이야기한다.
우리는 그렇기에, 오차 행렬을 요구해야만 한다.
오차 행렬(혼동 행렬, confusion matrix), TP, TN, FP, FN
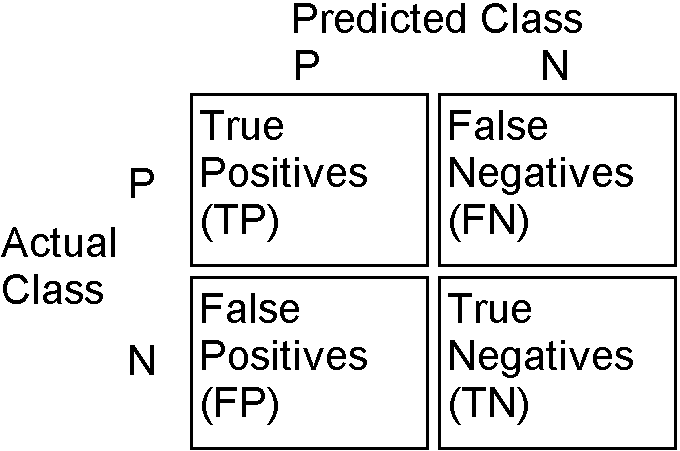
먼저 이 표를 구성하는 방법은 간단하다.
먼저 뒤 P와 N을 확인한다.
- 모델이 긍정을 예측했는가? -> P
- 모델이 부정을 예측했는가? -> N
그리고 앞부분을 채운다. - 모델이 실제 예측대로 맞췄다 -> T
- 모델이 실제 예측과 다른 오답을 예측했다 -> F
오차 행렬에서 구할 수 있는 주요 지표는 다음과 같다.

그런데, 위 네가지 정보를 다 활용하는 정확도의 경우, TN에 지나치게 크게 영향을 받아 오해를 불러일으키고 있다.
큰 집합인 TN에 영향을 받지 않고 모델을 평가할 수 있는 방법이 없을까?
F1 score
F1-score은 다음 식으로 구할 수 있다.
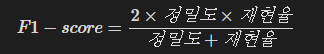
이는 정밀도와 재현율의 조화평균으로 구해지며, 큰 집합인 TN의 영향을 지움으로써 원하는 지표를 도출할 수 있다.![[image-13.png]]
베이즈 정리와 분류
2장의 베이즈 정리가 기억나는가?
베이즈 정리를 사용해 외부 정보로부터 오차 행렬의 결과를 추가로 검증할 수 있다.
다음은 환자 1000명의 오차 행렬이다.
| 테스트 결과: 양성 | 테스트 결과: 음성 | |
| 질병에 걸린 환자 | 198 | 2 |
| 질병에 걸리지 않은 환자 | 50 | 750 |
질병에 걸린 환자 중에서 99%를 성공적으로 식별한다.

그렇다면 양성 판정을 받은 사람 중 몇 퍼센트가 질병을 갖고 있을까?
이미 오차 행렬에 필요한 데이터가 전부 있기 때문에, 다음과 같이 조건부 확률을 뒤집어 정의할 수 있다.

일단 79.8%는 나쁘지 않은 수치이다.
그런데, 우리가 구하고자 하는게 "실제 질병에 걸린 사람 중 양성 판정을 받은 사람의 비율"인가?
일부 연구에 따르면 실제로 "인구의 1%"가 이 질병에 걸렸다고 한다. 여기서 베이즈 정리를 사용해서 우리가 실제로 원하던 양성 판정을 받은 사람 중 실제 질병에 걸린 사람의 비율을 구해보자.

계산 결과, 양성 판정을 받은 사람 중 실제로 이 질병에 걸렸을 확률은 3.39%에 불과했다.
진짜 양성을 성공적으로 식별할 확률이 3.39%에 불과하다면, 이 테스트는 사용하지 않는 것이 좋을 것 같다.
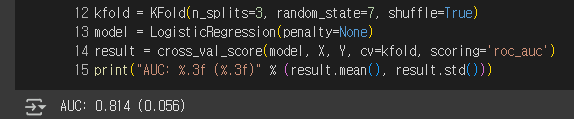
ROC 곡선과 AUC
다양한 머신러닝 모델을 평가할 때 수십, 수백 또는 수천 개의 오차 행렬이 만들어질 수 있다.
이러한 행렬을 일일히 검토하는 일은 매우 지루하므로 ROC 곡선을 이용해 행렬을 요약할 수 있다.
ROC 곡선

- receiver operator characteristic curve
- 한국어로 번역하면, "수용자 작용 특성 곡선"일라고 한다.
- 검은 점은 각 테스트 표본을 의미한다.
- x축은 "진짜 양성 비율(재현율, TP/(TP+FN))"를 의미한다.
- y축은 "거짓 양성 비율(FP/(TN+FP)"을 의미한다.
ROC 곡선은 AUC와 같이 쓸 때 그 위력을 발휘한다.
AUC
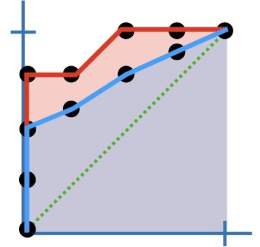
- Area Under the Curve
- 여러 모델을 비교할 때 사용하는 지표이다.
- 곡선 아래 영역의 크기를 비교해 더 넓은 쪽을 고평가한다.
AUC를 평가 기준으로 사용하고 싶다면, 다음과 같이 코드를 작성하면 된다.